The Department of Mathematics and Science Education

tiffani c. knight

For this particular assignment, I explored Bouncing Barney’s journey in a triangular room. Some info: Barney is in a triangular room. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.

My goal is to prove that Barney will eventually return to his starting point and to find out how many times Barney will run into a wall before returning to his starting point.

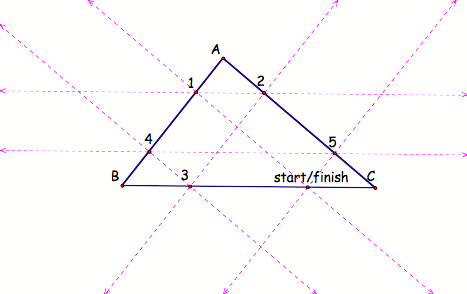
The diagram above outlines Barney’s journey. You will notice that he does eventually return to his starting point. If you don’t count the ending wall, Barney runs into 5 walls, two on each side, except where he started, but if you count the ending wall, then he would have run into 6 walls, two on each side of the triangle.

I wonder what would happen if Barney started from the midpoint of BC. I constructed the midpoint of BC and drug the starting point to that midpoint. Here’s what I got:

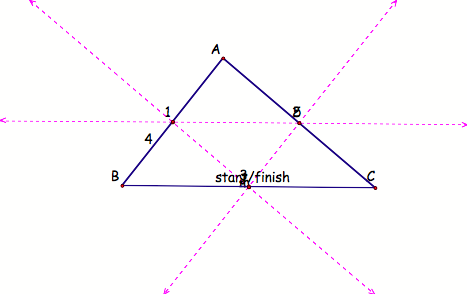
Again, Barney does return home, and he returns home faster this way. He only runs into 2 walls (3 if you count the ending wall). Seems like if you start at the midpoint, then you cut the number of walls hit in half.

If Barney starts at a point on a line that goes through BC (he’s starting outside of triangle ABC), then he will be walking all day and night; he will not return to his original starting point and he does not run into any walls of the triangle. And this is because his path is parallel to side AC:

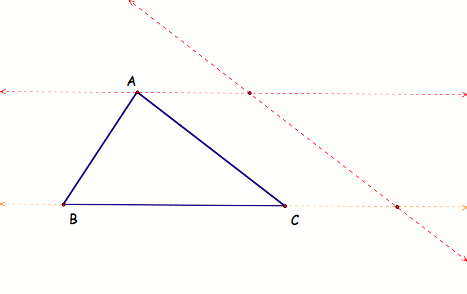
Let’s explore Barney’s path when he starts at vertex C.

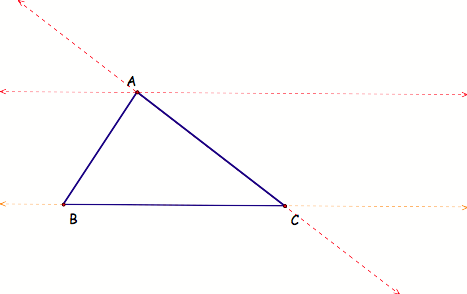
This graph shows us that Barney does hit 1 one, but then he doesn’t hit any other walls because, regardless of whether he goes left or right, he walks off into space, parallel to AC, which means that he will never run into AC.

Let’s go back to when Barney started at a point outside of the triangle. Let’s make some extensions of the segments and see what happens:

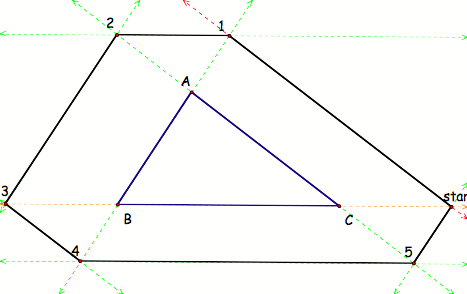
Well, it looks like when we make some extensions, it doesn’t matter if Barney starts outside of the triangle. He still makes it back to where he started and in the same amount of wall hitting as when he started on a point on BC (not the midpoint). His path is outlined in black. It forms a hexagon. I take it that has something to do with how many walls he hit (including end point). That’s interesting.

I scrolled up to see if this was true for the other graphs, and it is. When Barney started at a point on BC, it took him 6 movements before he returned, and this path forms a hexagon. When he started from the midpoint, it took him 3 walls to end up where he started, and that path creates a triangle.