Andy and George had three and five cookies respectively. They decided to eat them together for a snack. Before they started to eat, Jimmy joined them. Since he did not have any cookies, Jimmy offered $8 to share the cookies. After they ate, George gave $3 to Andy and kept $5 for himself. But Andy did not accept $3, and asked for more. If you were the judge, what would be your conclusion for this case? In other words, was the sharing between George and Andy (i.e. $5 and $3 respectively) fair?

Analysis

A common answer at the first sight to this case would most probably be that the sharing of $8 between George and Andy as $5 and $3 respectively is fair. Because, George had 5 cookies so he should take $5 out of $8. And the remaining $3 should go to Andy who had 3 cookies. Unfortunately, any judge who knows math would probably decide that the sharing is not fair. Why? Follow this...

Since we do not know how much cookie each person ate, we have to assume that each ate equally. Thus we have to divide each cookie into 3 equal piece. Since we have 8 cookies, there are totally 3*8 = 24 pieces. More precisely, since Andy has 3 cookies, he actually contributes 3*3 = 9 pieces. Accordingly, George contributes 5*3 = 15 pieces. If each person eats equally (i.e 24/8 =8 pieces), Andy eats 8 pieces out of his 9 pieces and there left 1 pieces. Likewise, George eats 8 pieces out of his 15 pieces and there left 7 pieces. Thus, Jimmy eats 1 piece of Andy's and 7 pieces of George's cookies. In that situation, Andy and George have to take $7 and $1 respectively in a fair sharing of the money. Therefore, the first sharing was unfair.

We can demonstrate the situation using a spreadsheet (Click Here for the file) as in the following figure

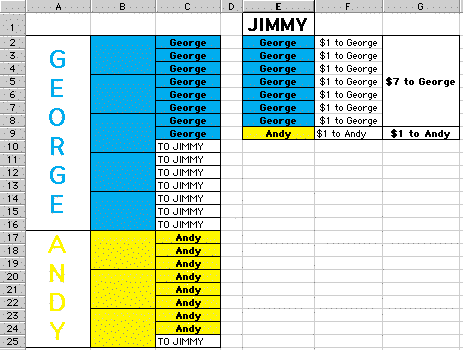
In the figure above, George's cookies and Andy's cookies are shown in blue and yellow respectively. Since there is three person, we have to divide each cookie into three. And the rest of the story goes like we have explained above.

Using spreadsheet, we can generalize the above "fair sharing algorithm" for any amount of money given by Jimmy for any number of cookies brought by George and Andy. The below figure shows the idea behind this process. In fact, there is nothing different in the logic that we explained above.

As we may notice, we add the number of cookies brought by George (See cell B2) and Andy (See Cell C2) in Cell BC3. Since there is three person, we divide this by 3 in Cell B4, C4 and D4. To find who gets how much, we first find how many third cookies (i.e., pieces) each person brings to share. We subtract the number of pieces that the person eats (i.e., cell B5 =C5 = D5). After that, we multiply that amount with D2/B5 which is the share of money for the number of pieces for per person.

Click Here for the spreadsheet file.

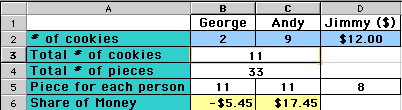
In the figure below, the distribution of $12 among George and Andy whom brought 5 and 3 cookies respectively. In the spreadsheet file, you can just enter any values for the # of cookies brought by George and Andy and any amount of money given by Jimmy.

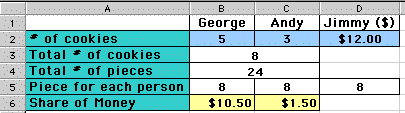
One also should notice that, in that generalized solution, one may get negative values in "Share of Money" cell. For example, if George brings 2 cookies while Andy brings 9, we may get that in a fair sharing George gets -$5.45 and Andy $17.45. This might seems bizarre at the first looking if we consider that the total amount of money brought by Jimmy is $12. Well, there is nothing wrong with this calculation. If we consider that everyone eats equal amount of cookie, then since George eats more than he brought, then he eats from Andy's and thus owes him exactly $5.45. In other words, And not only should get $12 brought by Jimmy but also should get $5.45 from George.