
Trivial Pursuit
By Rebecca L. Adcock
Student teaching is over but our class has been assigned to observe in middle schools over a three county area. It gives us exposure to students younger than the ones most of us taught during our student teaching stints in senior high schools. It has been an interesting experience. I am at a Title I school and my sixth-graders come to class better prepared than the high school students. The younger kids actually bring paper, pencils, and their textbooks to class! I will admit, though, that they really love the noisy, disruptive electric pencil sharpener.

J.E. Richards Middle School
The students attend a class that is called ‘CQI’. That
stands for Continuous Quality Improvement. Each student attends a CQI class for
the subject that they struggle with the most. Since my mentor teacher, Tammy
Thompson, has taught in an alternative school, she is experienced in teaching
struggling learners. In fact, she will have some involvement in writing
curriculum for next year’s CQI and
she hopes to drum up some support for an idea she is passionate about. From her
studies and her experiences, she has concluded that the hour spent in CGI is
most beneficial to the student if
it is spent previewing the concepts and vocabulary the student will soon
encounter in his/her regular mathematics class.. The struggling student, having
already seen some of the material, is more prepared to grasp the concepts, keep
up with the rest of the class and as a result feels more successful. The class
is currently used to follow up on past class work
Now that you’ve “got
the picture”, I want to describe a
lesson that the CQI class worked on and some of the questions that I had that
arose as a result and some of the ideas the lesson invoked.


Tammy Thompson and class. Some
of our “free spirits”!
The students were still grappling with the concepts of
area and perimeter of polygons so Ms Thompson assigned the students to create
as many polygons as they could imagine, using twelve one-inch plastic squares.
They could create both regular and irregular polygons (and some were highly
irregular!) and they had to document their shapes on graph paper and
‘calculate’ the perimeter of each. Since each tile had an area of one, they
knew that the area of each shape would be 12 square inches. Here’s one
student’s paper:
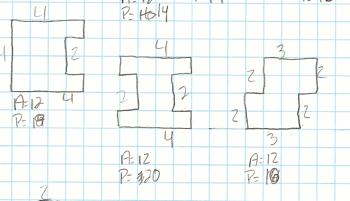
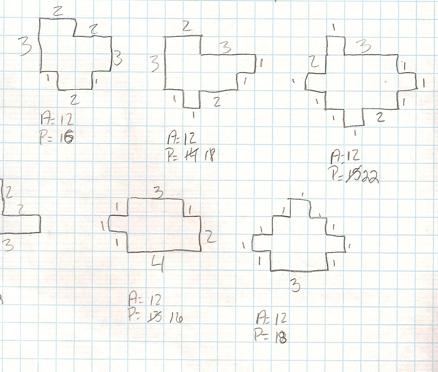
And another student’s…
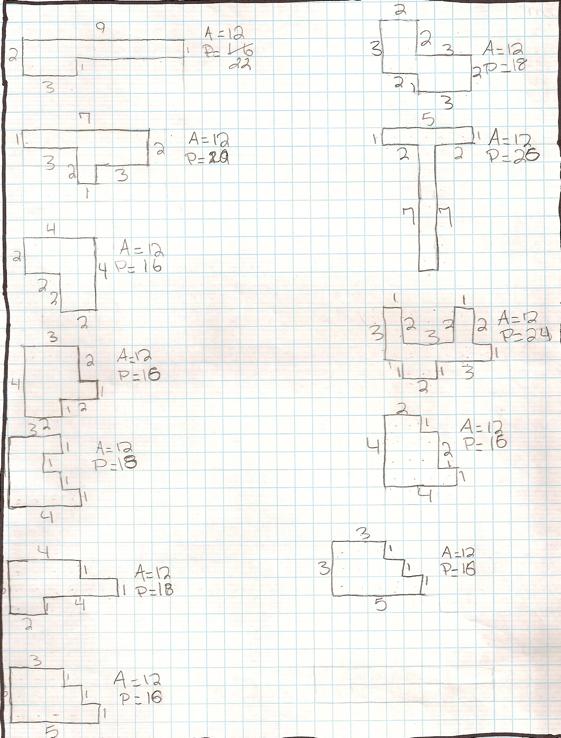
Although it may not have been
apparent to the students, I noticed that given a polygon created by 12 squares,
the perimeter was always an even number. The students may not have noticed the
pattern because they were still having trouble computing the perimeters. I saw
a lot of promise in how this lesson could be expanded and turned into a
classroom investigation.
Here’s how it could go…
One of the questions that may
arise would be the definition of a polygon. In sixth grade, the students are
exposed to regular polygons but the shapes they were creating did not look
“regular”. Some of the shapes above would work very well into the following
definitions:
Š
A polygon is a closed plane figure whose sides are line
segments that intersect only at the endpoint.
Š
A convex polygon is a polygon in which any segment connecting any two
vertices lies inside of the polygon.
Š
A concave polygon is a polygon in which at least one segment connecting
two vertices lies outside of the polygon.
Once the students
have created a number of shapes, ask them to speculate on anything interesting
that they have noticed. For example, a student may have noticed that the area
is an even number, and all the perimeters on his shapes are also even numbers.
If the area was odd, would the perimeter be odd? The students would draw more
shapes, this time using 11 squares…
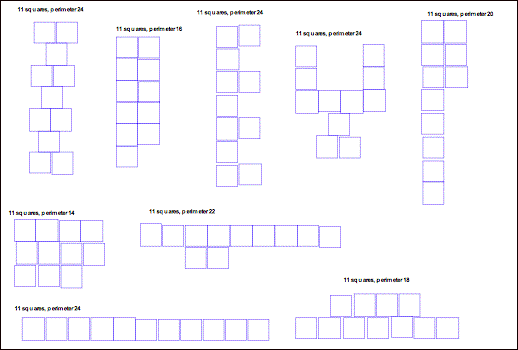
Once again the perimeters are
all even. So where would the investigation go from here? Perhaps half of the
class would continue to investigate shapes composed of a different number of
squares, while the other half uses a different shape, like a triangle, that has
an odd-number of sides, rather than the even-number of sides. The problem with
using an equilateral triangle with a side-length of 1 is that the area of that
triangle is not equal to 1. So our project changes from comparing area to
perimeters to comparing the number of figures to the perimeter. This could lead
to an introduction of the Pythagorean Theorem, which would be needed to
calculate the area of the triangle. More investigations…
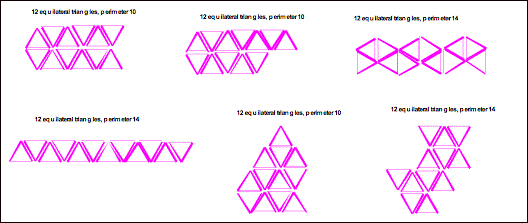
So using an even number of
odd-sided figures would create an even perimeter. What if an odd number of
odd-sided figures was used?

Finally an odd perimeter! It
worked for 11 triangles and worked again for 7 triangles.
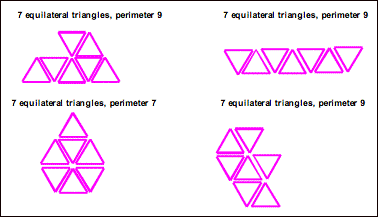
So we finally end up with a
conjecture. It appears that a figure created from an odd number of odd-sided
shapes will have a perimeter that is an odd number. An even number of odd-sided
shapes, an odd number of even-sided shapes, and an even number of even-sided
shapes all create figures with a perimeter that is an even number.
“So what?”, the students ask.
Well, I don’t really know the significance so let’s look at the number of
shared sides in each figure and see it any patterns appear. We can put all of
our numbers into a spreadsheet and see if we can discover a pattern.
|
Sided Shape |
Number of Shapes Used in Figures |
Perimeter |
Number of Common Sides |
|
3 |
7 |
7 |
7 |
|
3 |
7 |
9 |
6 |
|
3 |
11 |
9 |
12 |
|
3 |
11 |
11 |
10 |
|
3 |
11 |
11 |
11 |
|
3 |
11 |
13 |
13 |
|
3 |
12 |
10 |
13 |
|
3 |
12 |
14 |
11 |
|
4 |
11 |
14 |
15 |
|
4 |
11 |
16 |
14 |
|
4 |
11 |
18 |
13 |
|
4 |
11 |
20 |
12 |
|
4 |
11 |
22 |
11 |
|
4 |
11 |
24 |
10 |
|
4 |
12 |
16 |
14 |
|
4 |
12 |
16 |
15 |
|
4 |
12 |
16 |
16 |
|
4 |
12 |
18 |
13 |
|
4 |
12 |
18 |
14 |
|
4 |
12 |
18 |
15 |
|
4 |
12 |
18 |
16 |
|
4 |
12 |
20 |
11 |
|
4 |
12 |
20 |
14 |
|
4 |
12 |
22 |
13 |
|
4 |
12 |
22 |
21 |
|
4 |
12 |
24 |
12 |
|
4 |
12 |
26 |
11 |
|
|
|
|
|
I can detect no patterns, but
does this mean that the exercise was a waste of time? Not in my opinion! Here
is a list of concepts and skills that could be taught through a lesson like
this, depending on what tools the teacher chooses:
Š
Definition of a polygon.
Š
Examples of convex and
concave polygons.
Š
Collecting (creating)
data.
Š
Detecting patterns.
Š
How to construct an
argument to support an idea.
Š
Constructing a table
with data in Excel or Word.
Š
Using the Pythagorean
Theorem.
Š
Using Geometer’s Sketch
Pad to construct a square and triangle and using Transform and Reflect.
I enjoyed the potential of
this lesson. The students were really engrossed in creating as many different
shapes as they could and that interest could have been channeled into a longer
lesson, complete with u-turns and pitfalls as the investigation developed. In
addition, it could have opened the door to introducing the students to
Geometer’s Sketch Pad and other software. Once that door was open, I could
imagine a second lesson that would involve the centers of triangles and Euler’s
line. Where this lesson turned out to be a trivial pursuit that failed to
develop anything of mathematical significance, the second lesson could end with
the “discovery” of a renowned geometric property.
Click on the square to see
how I constructed one in GSP for the examples above.
Click on the triangle to see
how I constructed one in GSP for the examples above.