Geometric Inversions

By Rebecca Adcock

Before we can look at geometric inversions, we must first learn something about the geometry of a circle.

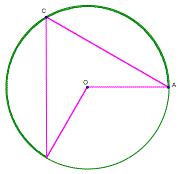
For any two points on a circle, a triangle formed with the center as the third vertex is an isosceles triangle. The two sides of the triangle that are radii of the circle are congruent. Click on the picture below to watch an animation in Geometer’s Sketchpad. Again mildly interesting…

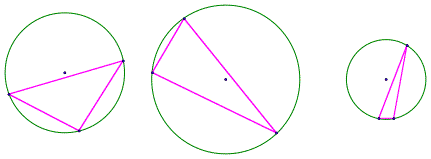
For any three points on a circle, a triangle can be constructed. This is just an extension of the fact that a triangle can be constructed from any three noncolinear points and three points on a circle are noncolinear. Mildly interesting but not exciting…

What is more interesting is that for every triangle, there is a unique circle that passes through all three vertices. To demonstrate that, we can find the circumcenter of any triangle and use it to construct a circle through the vertices. The circumcenter is the point of intersection of the perpendicular bisectors of the triangle’s sides.

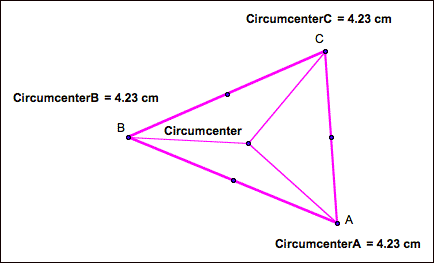
Notice that the circumcenter is equal distance from each vertex. So we can create this circle…

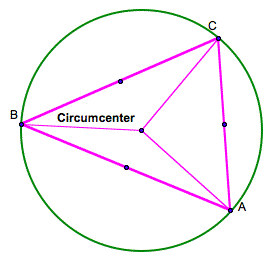
Now this starts getting into interesting stuff but I’ve already investigated this topic. To see more on this, visit my EMAT6680 work.

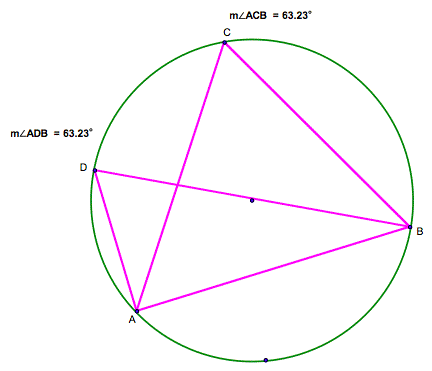
Let’s look at some of the angles that occur within a circle. For example, we can look at the same triangle in the picture above and look at the angles BCA and BOA. Angle BOA is a central angle, that is, the vertex is at the center of the circle.

The pictures below demonstrate the following:

Given two angles within a circle that are formed by rays that intersect the circle at the same points, A and B, one angle having its vertex on the circle (point C) and the second having its vertex at the center of the circle (point O), then the central angle has twice the angle measure as the other or .

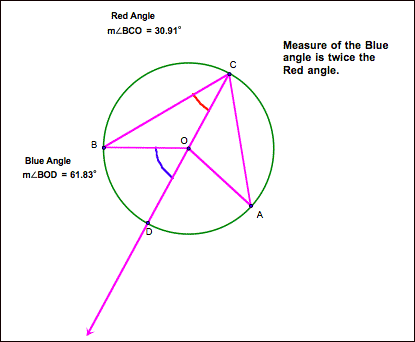
Let’s re-label the angles and state the demonstration as a proof.

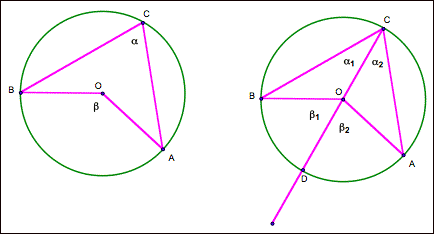
Click on this circle to watch a demonstration of the relationship between the angles we have defined as alpha and beta.

Here’s a second demonstration. Notice that our claim works for all positions of points A, B, C on the circle.

Wherever we choose point A, its measure will always be half the measure of the center angle.

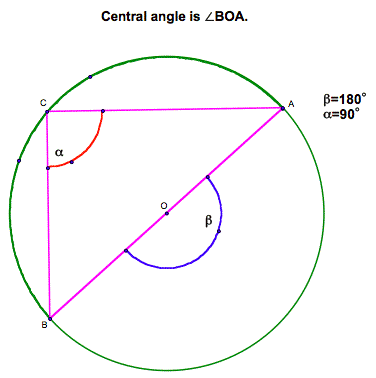
From what we now know, we can demonstarte that if two angles above the chord of a circle are equal, as in the picture below, then all four points will fall on a circle.

In the sketch below, I added some lines to the sketch above. First I drew a line through points C and D. Then I drew one through B and A. The lines intersected outside of the circle and I called the point of intersection P.

Turns out that this construction has some important relationships. Let’s look at two triangles formed by the intersecting lines…

Click on this picture to watch a demonstration...

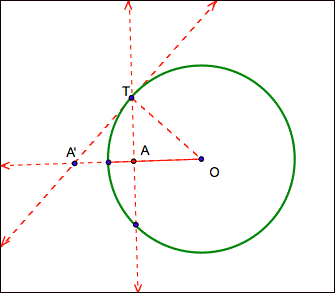
If a point A resides inside a circle, we can geometrically construct A’ as follows:

1. Given a circle with center O and any point A within the circle.

2. Construct a ray from O through A.

3. Construct a line perpendicular to the ray at A. Call the intersection of this line with the circle “T”.

4. Draw the radius from O to T.

5. At T, construct a line perpendicular to the radius. This line is tangent to the circle at point T.

6. The intersection of the tangent line with the ray is A’.

If a point A resides outside a circle, we can geometrically construct A’ as follows:

1. Given a circle with center O and any point A outside the circle.

2. Construct a ray from O through A.

3. Draw a line from A, tangent to the circle. Call the point of tangency “T”.

4. Construct a line through T that is perpendicular to the ray through O and A.

5. At T, construct a line perpendicular to the radius. This line is tangent to the circle at point T.

6. The intersection of the perpendicular line with the ray is A’.

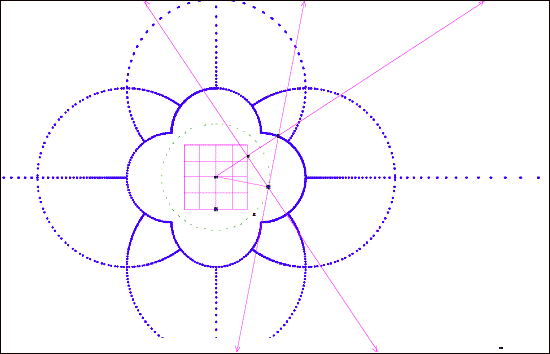
This has been only an introduction to inverses. There are a lot more serious topics to explore but let’s stop here and look at something a little less serious, the connection of math with art…

This was created by tracing the inverse point of the grid.

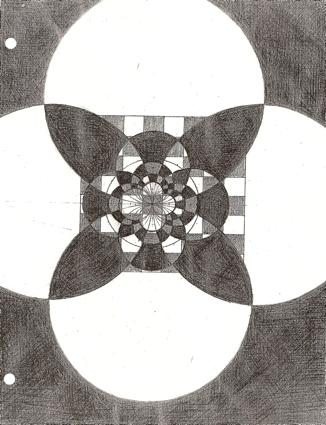
Here’s a similar project drawn by hand. This is not my own work. This was created by a mathematics professor at the University of Georgia.

Here’s how it begins…

The picture on the left shows the original grid behind the inversion. The picture on the right shows the final work, the inversion of the grid.

Return to Main Menu