Final Project

By Rebecca L Adcock

 

Statement of Problem:

Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

 

Exploration Section A:

Here’s the triangle I’ll be working with.

 

 

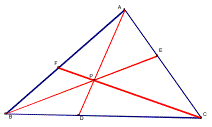
The line segments represented in the products (AF)(BD)(EC) and (FB)(DC)(EA) alternate around the triangle. Locate the segments on the above triangle and you’ll see what I mean. Is that significant? We’ll try to find out.

Watch an animation of this triangle with point P moving on the triangle’s incircle. Stop the animation periodically and compare the products. (AF)(BD)(EC) always equals (FB)(DC)(EA) so the ratio of the two products is always 1. Is that significant? Most likely, or Dr. Wilson wouldn’t have us trying to prove it.

 

Click on the figure below:

 

Conjecture:

Given any triangle ABC and an interior point P, with line segments constructed from each vertex, through point P and intersecting the opposite side, the product of the ratio of the side segments (as given above) is one.

 

Back to my working triangle…. I’ve hidden the lines I used to construct my interior segments so let’s make those visible and construct a couple of parallel lines. As a result, we should have several triangles to investigate.

 

           

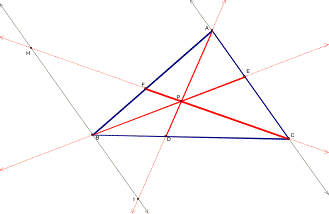
I’ve set up two parallel lines: one through point B and parallel to side AC of the triangle and the other is an extension of side AC.

 

Pair #1: Similar Triangles BIP and AEP

 

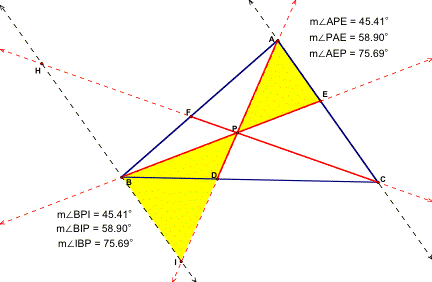
We know that these two triangles are similar because of the AAA postulate: If the three angles of a triangle are congruent to the three angles another triangle, the two triangles are similar. We also know that the angles of these two triangles are congruent because of the properties of parallel lines cut by a transversal. i.e. alternate interior angles are congruent (<IBP and <AEP, <PAE and <BIP) and vertical angles are congruent (<APE and <BPI).

Since the triangles are similar, the corresponding sides are proportional.

   

BI/EA=1.39       PB/PE=1.39       PI/PA=1.39        …so BI/EA= PB/PE= PI/PA.

 

Pair #2: Similar Triangles BHP and CEP

 

 

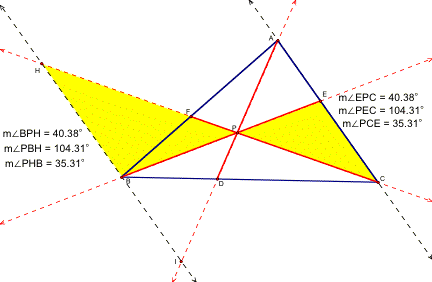
We know that these two triangles are similar because of the same arguments we used in Pair #1. The alternate interior angles here <PBH and <PEC, <PCE and <PHB and the vertical angles are <BPH and <EPC.

Since the triangles are similar, the corresponding sides are proportional.

              

BH/EC=1.39      PB/PE=1.39       PH/PC=1.39      …so BH/EC= PB/PE= PH/PC

 

Pair #3: Similar Triangles HIP and ACP

 

 

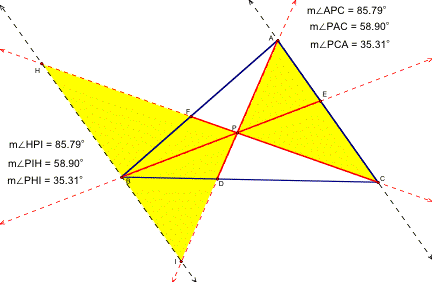
Again we know that our two triangles are similar because of the AAA postulate. The alternate interior angles are <PIH and <PAC, <PHI and <PCA and the vertical angles are <HPI and <APC.

Since the triangles are similar, the corresponding sides are proportional.

              

PH/PC=1.39      PI/PA=1.39        IH/AC=1.39       …so PH/PC= PI/PA= IH/AC

 

Pair #4: Similar Triangles BDI and ACD

 

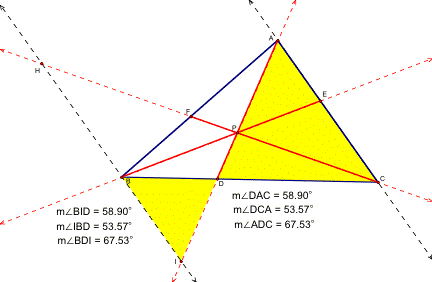
We know that our two triangles are similar because of the AAA postulate. The alternate interior angles are <BID and <DAC, <IBD and <DCA and the vertical angles are <BDI and <ADC.

Since the triangles are similar, the corresponding sides are proportional.

                           

DA/DI=1.68       DC/DB=1.68      AC/BI=1.68       …so DA/DI= DC/DB= AC/BI

 

Pair #5: Similar Triangles BFH and ACF

 

 

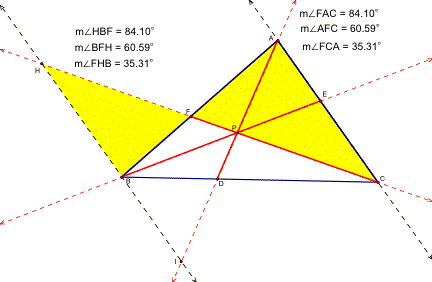
We know that our two triangles are similar because of the AAA postulate. The alternate interior angles are <HBF and <FAC, <FHB and <FCA and the vertical angles are <BFH and <AFC.

Since the triangles are similar, the corresponding sides are proportional.

                           

FC/FH=1.25      FA/FB=1.25      AC/BH=1.25      …so FC/FH= FA/FB= AC/BH

 

Exploration Section B:

Below is a representation of how the triangle with point P looks when the triangle is constructed with lines instead of line segments. The next three show what happens when point P moves outside the triangle.

 

 

 

 

 

 

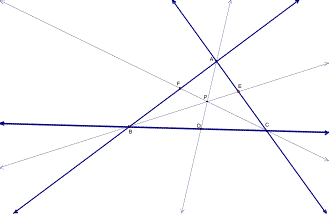
To see point P move around the circumcircle of the triangle, click on the figure below. Remember to watch the product ratio.

 

Exploration Section C:

 

When point P lies inside triangle ABC, the ratio of the area of triangle ABC to the area of triangle DEF is greater than or equal to 4. Here are three examples:

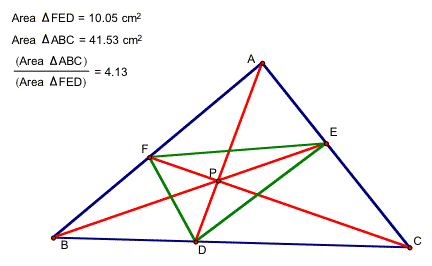
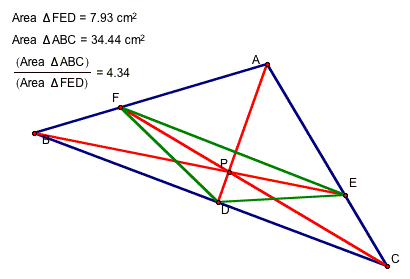
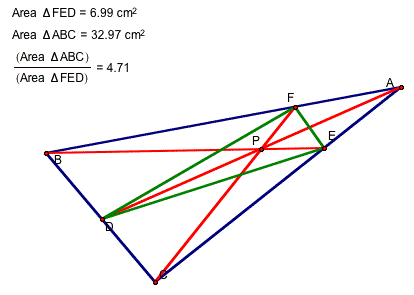
To manipulate this yourself, click on the figure below. Move the vertices of triangle ABC and point P. Watch the ratio.

 

            As a final point, look what happens when point P coincides with the triangle’s centroid. (Ratio of the areas is 4.)

 

            Click here…

 

 

            Return