Polar equations have nothing to do with big white bears that live in cold places. So what are they? (I had to look this up in a textbook; polar equations were invented after I earned my BA.)

We just finished looking at parametric equations in Assignment 10 and polar equations are another way of looking at parametric equations (or vice versa).

According to Algebra and Trigonometry by James Stewart, Lothar Redlin, and Saleem Watson (page 803)….

POLAR EQUATIONS IN PARAMETRIC FORM

The graph of the polar equation r=f(theta) is the same as the graph of the parametric equations

x=f(t) cos t y=f(t) sin t

Let’s take a look at

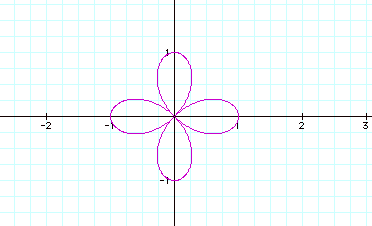
When n is an integer, this form is called the n-leaf rose.

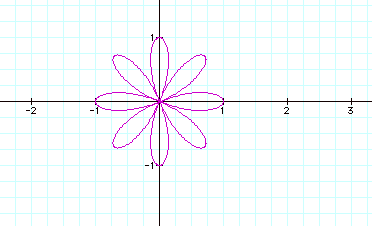
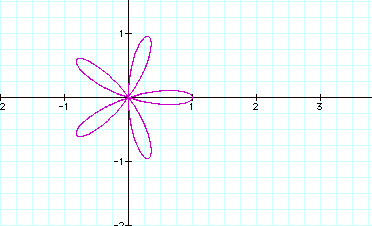
We can very quickly see a pattern here.

is a n-leaved rose if n is odd or a 2n-leaved rose if n is even.

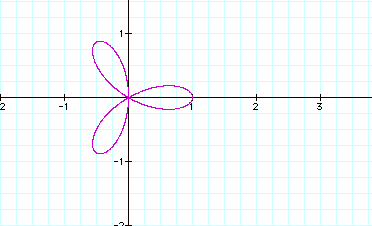
What happens if we replace cos with sin?

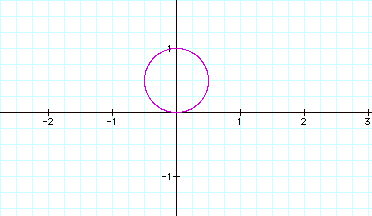
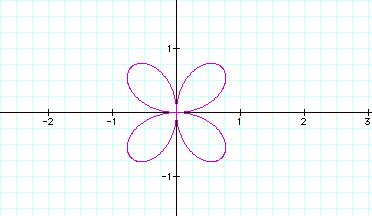
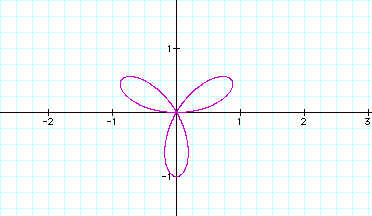
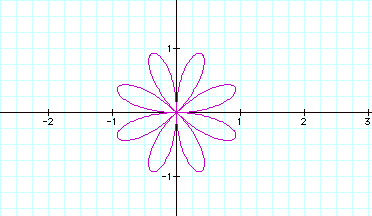
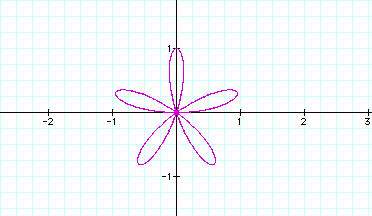
Our earlier conclusion on the relation of number of leaves to the coefficient of theta holds true. The orientation of the figure to the axes changed when we changed cosine to sine

Let’s see what happens with the following equation when we vary a,and b .

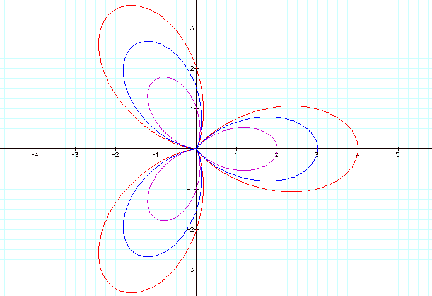
a>b This shows a 3-leaf rose where b= 1 and a varies from 1 to 3 in increments of .25.

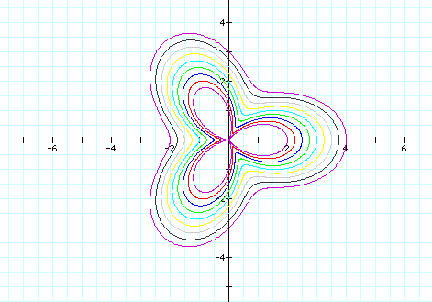
a<b This shows a 3-leaf rose where a=1 and b varies from 1.25 to 2 in increments of .25.

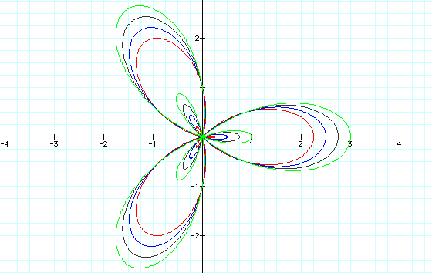
a=b This shows a 3-leaf rose where a=b and the value ranges from 1 to 2 in increments of .50.

We have seen that increasing the value of a over b results in decreasing the definition of our figure. The leaves appear to ‘smooth out’. Increasing b over a gives our figure more definition.

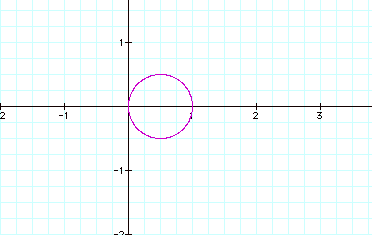
We’ve only seen a sample of polar equations. Let me leave you with one more interesting figure. Looks what happens to the 1-leaf when a=1 and b is greater. Would the figure eventually become a circle?

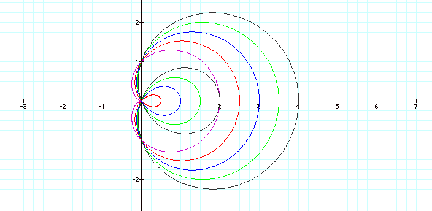
See ya…

Return