Assignment
4: Center Secrets of
Triangles
By
Rebecca L. Adcock
Construct four centers of a
triangle, the Centroid (G), the Orthocenter (H), the Circumcenter (C) and the Incenter
(I).
The Centroid is the
intersection of the three medians.
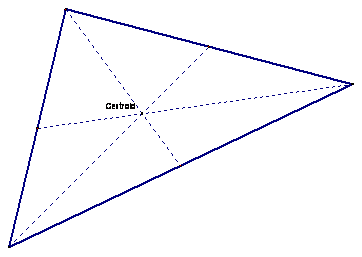The dotted lines are the medians. A median is a line
segment that connects the vertex with the midpoint of the opposite side.
Click and play.
The Orthocenter is the point
where the three altitudes of the triangle intersect.
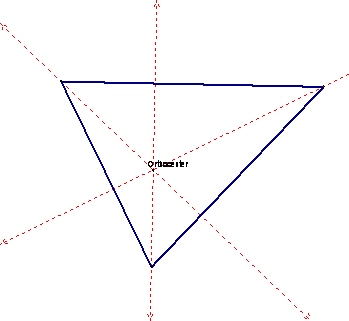The altitude is a perpendicular line segment from the
vertex to the opposite side.
Click and play.
The circumcenter
is equidistant from all three vertices. It lies on the perpendicular bisectors
of the three sides. Sometimes it lies outside the triangle. It is also the
center of a circle (Circumcircle) that contains the
vertices.
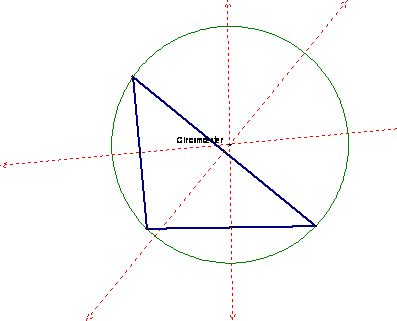Click and play.
The Incenter
is equidistant from all three sides of the triangle. It lies
on the angle bisectors. It is also the center of the inscribed circle (Incircle).
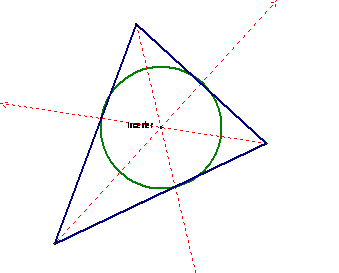Click and play.
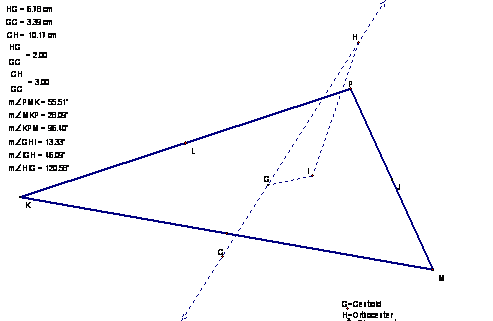
Now let’s put all these
centers into the same triangle and see how they relate to each other.
Here’s what I found:
- The centers always “line up” in this order: HIGC.
- I and G always remain in the interior of the
triangle.
- H and C sometimes lie outside the triangle.
- H is always the closest center to an obtuse
angle.
- C is always the farthest center from an obtuse
angle.
- In a right triangle, H lies on the vertex and C
lies on the midpoint of the opposite side.
- H,G, and C always lie on
a straight line.
- The ratio of line segment HG to line segment GC
is always 2.
- The ratio of line segment CH to line segment GC
is always 3.
- The measure of angle HIG is always greater then
90 degrees.
This one is really great to
play with.
We can construct triangles
inside triangles. If we connect the midpoints of the sides of a triangle, the
result is the medial triangle.
More discoveries:
- The triangles share a centroid.
- The orthocenter of the medial (red) triangle
coincides with the circumcenter of the large
triangle.
- Each side of the medial triangle is parallel to a
side of the larger triangle.
Check it out for yourself.
