Assignment # 7: Off On a Tangent

By Rebecca L. Adcock

 

 

 

In this assignment, we are attempting to construct a circle that is tangent to two given circles. The first step is to conceptualize how to construct the tangent circle.

 

Given this construction (below left), we want to construct a third circle (red) that is tangent to each of the given (green) circle.

 

                                                                                                                 

                                                                       

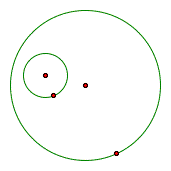
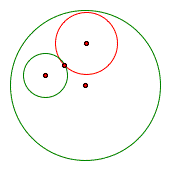
              There are an endless numbers of circles that are tangent to the two given circles (shown in green). The picture above shows just one instance of a circle tangent to the two given. The red circle is what we want to construct so precisely that it touches each of the other two circles at a single point. What we have drawn here is just a rough sketch of our objective.

              One way to create a circle is to use a point as the circle’s center and a line segment as its radius. Our problem is that we don’t know where to place the center and we don’t know the length of the radius. We will have to use known properties of our given circles to determine our unknowns.

              Let’s go back to our given circles and see what we can figure out.

 

                        Here, (left) I have created a radius in our smaller given circle. I chose a point on our larger given circle to be the point of tangency for our desired circle. Then I created a second circle (the blue one) using the chosen point and the radius. Now I have two small circles that are congruent. I need to find a point that is equally distant from the perimeter of the small green circle to the chosen point of tangency on the big green circle.

             

 

            Besides the two given circles, we have other known constructions we can use. We have three points, each one is the center of a circle. It only takes two points to draw a line. Given a line and a point, we can draw a parallel or perpendicular line. Given three points, we can draw a triangle. Given a triangle, we can use its properties to construct other figures. We’re on a roll now!

 

I’m going to cheat a bit here. I already know which points to use to draw the line we need. That’s the nice thing about studying a science that’s been around for a couple of thousand years. Someone else has already figured out a lot of this stuff so we just walk in their footprints. The fun part is, once we construct our figure, we can experiment around with it and see what we can discover about circles. (Ask me later and I’ll tell you how I ‘discovered’ the “Oiler” Line.) Anyway, Here’s the lines I constructed.

 

                       

 

Line J was constructed through the radii of two of our circles. It also provides us with an intersection point on the outside of our constructed (blue) circle that will be one vertex of an isosceles triangle. The second vertex of the isosceles triangle is the center of the smaller given circle. We will find the third vertex by creating a line perpendicular to line segment K at its midpoint. Where that perpendicular line intersects J is the third vertex of the triangle and the center of our desired circle. I’ll stop talking now and draw it for you.

 

 

 

 

             
Our red circle is only one of an infinite number of circles that are all tangent to the two given circles. To see many circles represented as a movie, click here.

 

Now that we have finally constructed our tangent circle, let’s see what we can discover about it. We’ll set a trace on the center of our red circle and see what happens as it moves along its ‘track’. Notice the differences in the red circle and its traces as the size and position of the given (green) circles change.

 

                         

Did you see what I saw?

• The center of our red tangent circle traces a flattened circle ( an ellipse?) as it moves around its track.
• Changing the sizes and positions of the given circles changes the trace, making it appear more or less circular.

 

Let’s try to make sense out of this. If you looked at the demonstrations, you remember that the dark red “flattened circle” (an ellipse?) is a trace that is drawn as our red circle moves around on its “tangency track”.

The dotted purple lines are the radii of the green circles.

The solid purple lines connect the centers of our two given circles to the center of our constructed circle.

 

 

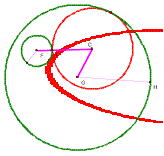
There’s something else going on here. Let’s look at this picture in action and check out some measurements.

Here’s what I saw:

• The sum of the solid purple lines never changes even though the two lines change in length.
• The sum of the dotted purple lines don’t change.
• The two sums are the same.
• Things like this don’t happen by accident in geometry. (That’s what’s so cool about it!)

 

We have actually demonstrated here that the trace we put on the center of our constructed circle is an ellipse. In geometry language: “The locus of the center of all circles tangent to the two given circles is an ellipse. An ellipse is a curve that is the locus of all points in a plane the sum of whose distances r1 and r2 from two fixed points f1 and f2 is a constant.”

 

It is real interesting that r1 + r2 (solid purple lines) is equal to the radii of the two green circles (dotted purple lines). We demonstrated that with our measurements. By the definition of an ellipse, we know that r1+r2 equals the length of the ellipse along its major axis. (That’s the blue line.) So the length of our ellipse along its major axis is equal to the sum of the radii of the given circle.

Guess what? I don’t know why. There’s a reason for it somewhere in all this…..

 

There’s a lot more exploring we could do with circles. Check out this one last sample and figure out the similarities and differences from what we’ve already seen.

 

                                                                                                           

See ya later.

 

Return.