Assignment 8: Investigating Altitudes and Orthocenters

By Rebecca L. Adcock

 

 

 

In previous assignments, we’ve looked at triangles, orthocenters, and circumcenters. In this lesson, we’re going to look at those objects again and see if we can find anything new. We can choose any three points and construct a triangle. We’ll call it ABC and we’ll also construct the orthocenter of the triangle.

 

 

 

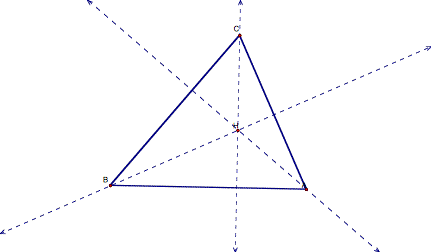
Review: We locate the orthocenter by constructing the triangle’s altitudes. The altitude is a line that passes through the vertex and is perpendicular to the side of the triangle opposite the vertex.

Above we have the triangle ABC with the orthocenter at H. the dashed lines are the altitudes. Where they intersect is the orthocenter.

 

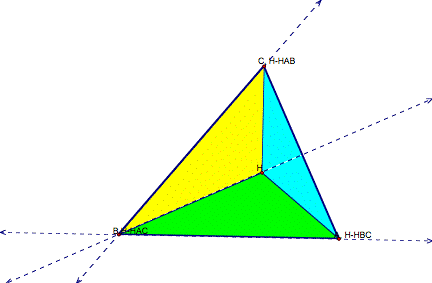
Now we’re going to look at the three triangles created by using the orthocenter as one vertex of each. Here’s what the three triangles look like. See below.

 

 

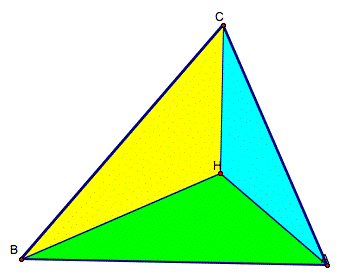
Now we locate the orthocenter for each of the smaller triangles. Before we begin, wouyld you care to speculate on the locations of the smaller triangles’ orthocenters? I was surprised by their locations and even reconstructed my original triangle in case I had made a mistake. But it was no mistake. Here’s what happened…..

 

 

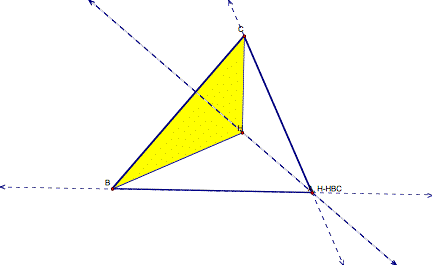
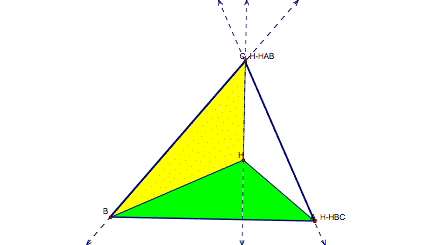
The orthocenter for each of the smaller triangles is one vertex of the original triangle.

 

 

 

 

Now let’s construct the circumcircle for the original triangle and for the three smaller triangles and see what happens.

 

Review: A circle can be constructed given a point and a radius. To create the circumcircle, we need to locate the circumcenter of the original triangle. The circumcenter is the intersection of the perpendicular bisector of each side of the triangle.

 

 

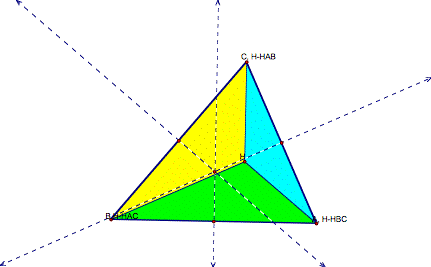
Above, we’ve located the circumcenter. So we have a point. How do we get a radius? Since the circumcenter is equidistant from the three vertices of the triangle, a line segment drawn from the circumcenter to any vertex could serve as the radius.

 

 

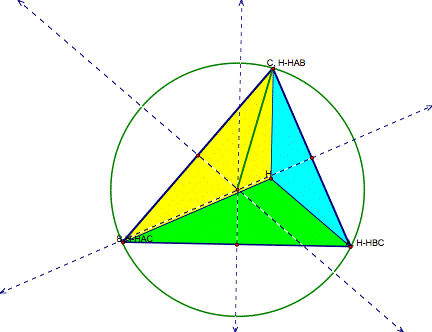
Here we’ve drawn the circumcircle given the center of the triangle (circumcenter) as the center of the circle and the line segment drawn from the circumcenter to a vertex of the triangle as the radius. (The green line segment visible in the yellow triangle is the radius. That just happens to be the one I chose. We could have used any one of the three.)

 

Now let’s construct the circumcircle of each of the smaller triangles using the techniques we used above. Since the yellow, green, and blue triangles are smaller than the original, I would guess that their circumcircles would be smaller than the one we just drew. What do you think?

 

Here is the circumcircle created for the green triangle.

 

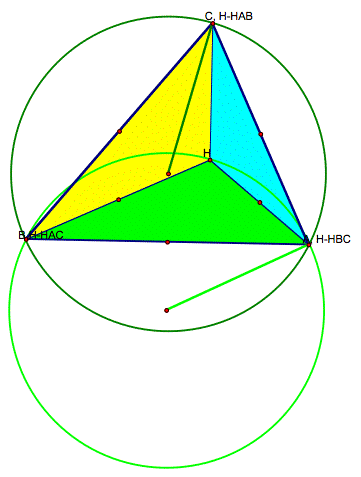
Here’s the circumcircle for the blue triangle….

 

 

 

And for the yellow triangle…

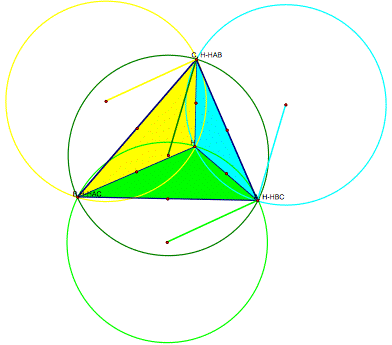
Above you see all four circumcircles for the four triangles.

And guess what? I was wrong. I had guessed that the three circumcircles for the smaller triangles would be smaller than the circumcircle for the original triangle. It appears that all the circumcircles are the same size.

 

Before we list our conjectures and conclusions for this exercise, let’s look at two more pictures. I was curious what would happen if we created a triangle using the centers of the fellow, blue, and green circles as the vertices.

 

 

 

Since the two triangles looked similar, I tested them by taking some measurements. (Measuring does not constitute proof in geometry, it just lets you know if you’re on the right track.) The two triangles are congruent. We’re on the track of something but I’m not sure what.

 

Then I wondered what would happen if we connected the 6 vertices of the two triangles.

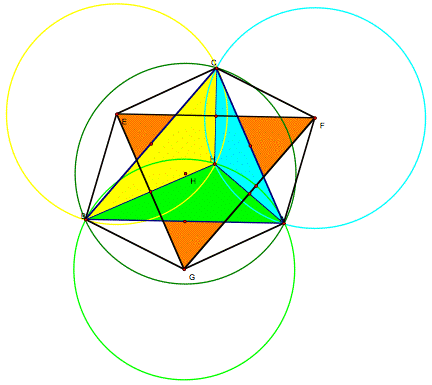
Now we’ve got a hexagon. It’s not a regular hexagon, which would have all sides equal and all interior angles equal. But it looks to me like the pairs of opposite sides may be parallel. Let’s check that out.

 

 

 

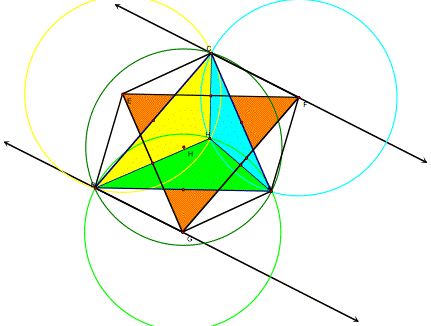
The two black lines were constructed individually as parallel to the opposite side . I also verified the other pairs of opposite sides.

 

Here’s what we’ve learned from this exercise.

Given a triangle ABC and its orthocenter H, we can construct three triangles HAC, HAB, and HBC such that:

1. the circumcircles for all four triangles are congruent.
2. the intersection of any two of the circumcircles belonging to the smaller triangles is a vertex of the given triangle ABC.
3. a triangle formed by connecting the centers of the circumcircles for HAC, HAB, and HBC is congruent to the original triangle ABC.
4. an interesting hexagon whose opposite sides are parallel and congruent is created by connecting the six vertices of the two triangles.

 

Return