Pedal Power

A Peek at Pedal Triangles

By Rebecca L. Adcock

Definition of a Pedal Triangle: Let triangle ABC be any triangle. Choose Point P as any point in the plane. Construct lines perpendicular to each side of the triangle that pass through P. The triangle formed by the intersections of the lines with the triangle is the Pedal Triangle.

******************************************************************************

If we choose Point P to also be the centroid of triangle ABC, we get this:

When triangle ABC is isosceles, the pedal triangle is similar. In the picture below BDE is the Pedal triangle. Line segment DE is parallel to line segment AC, sides are proportional and angles are congruent.

As triangle ABC approaches an equilateral triangle, the pedal triangle becomes identical to it. Below is a picture of the two almost being identical. Any closer and they will merge into one.

If we choose Point P to be the incenter of the triangle, we can get this:

The given triangle here in blue is isosceles. As it approaches equilateral, the pedal triangle merges with it.

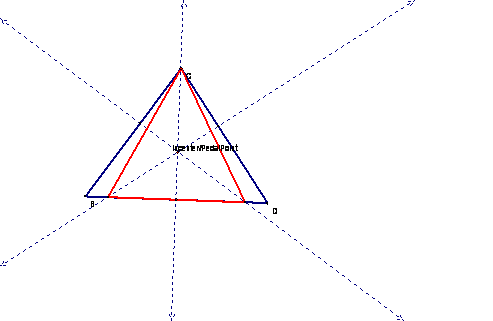
If we choose the orthocenter as the Pedal Point…….

…the Pedal Triangle and the given triangle are the same. As you can see, the only intersection of the lines thru the pedal point and perpendicular to the sides of the triangle are at the vertices.

If we choose to locate the orthocenter outside of the triangle also have it be the pedal point, the same thing happens. The pedal triangle and the given triangle are one and the same. Once again the only intersections occur at the vertices.

If P is the circumcenter….

… and the triangle is a right triangle, the pedal triangle is a line segment. The circumcenter-pedal point lies on one side of the triangle.

Here’s another case where the pedal triangle is a line segment. The third vertex lies outside the triangle past the vertex opposite the segment.

Here’s a more ‘normal’ looking pedal triangle.

Let’s try something more interesting with these pedal triangles. We will locate the midpoints on the sides of the pedal triangle and trace the locus of these midpoints as the pedal point moves on a circle centered at the circumcenter. First we’ll see what happens when the circle is larger than the circumcenter.

Here’s what the triangles look like with the traces of the midpoints. The locus are ellipses and partial ellipses.

The blue is the given triangle. The green triangle is the pedal triangle. The red are the locus of the midpoints.

To see this in action, click here.

If we use the circumcircle as the path…

… the trace ellipses look a little more complete. To see this in action, click here.

If we use a path smaller than the circumcircle….

… the ellipses are complete. To see this is action, click here.

Return