From the sketch alongside we can see that: (AF)(BD)(CE) =(BF)(CD)(AE) for any position inside of triangle ABC.

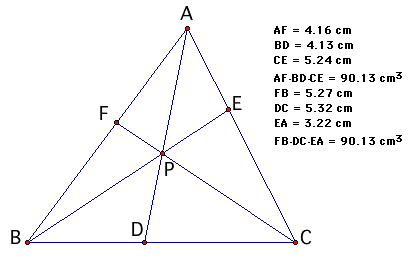Required to Prove: (AF)(BD)(CE) =(BF)(CD)(AE)

Proof: I am going to try to make this proof more visual that algebraic. Here we go:

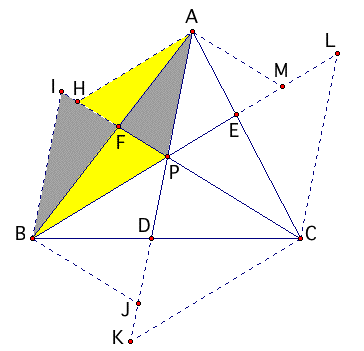
By drawing BI // AP and AH // BP we get the following similar triangles: triangle AFP /// triangle BFI triangle AFH /// triangle BFP From these similarities flow the following proportions: AF / BF = AP / BI ....................(1) AF / BF = AH / BP ....................(2) therefore AP / BI = AH / BP ....................(3) also AF = (BF)(AP) / BI ....................(4) AF = (BF)(AH) / BP ....................(5)

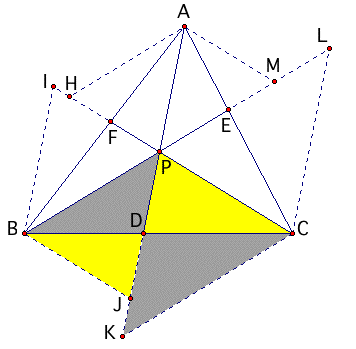
By drawing BJ // CP and CK // BP we get the following similar triangles: triangle BDP /// triangle CDK triangle BDJ /// triangle CDP From these similarities flow the following proportions: BD / CD = BP / CK ....................(6) BD / CD = BJ / CP ....................(7) therefore BP / CK = BJ / CP ....................(8) also BD = (CD)(BP) / CK ....................(9) BD = (CD)(BJ) / CP ....................(10)

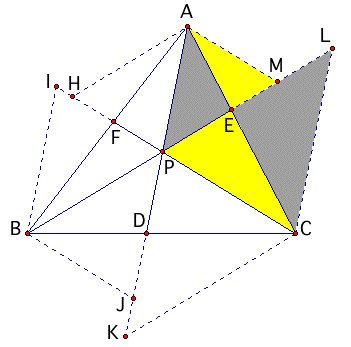
By drawing CL // AP and AM // CP we get the following similar triangles: triangle CEP /// triangle AEM triangle CEL /// AEP From these similarities flow the following proportions: CE / AE = CP / AM ....................(11) CE / AE = CL / AP ....................(12) therefore CP / AM = CL / AP ....................(13) also CE = (AE)(CP) / AM ....................(14) CE = (AE)(CL) / AP ....................(15)

From the 15 equations above we get

(AF)(BD)(CE) =[(BF)(AP / BI][(CD)(BP) / CK][(AE)(CP) / AM] using equations (4) , (9) and (14)

If we rearrange the righthand side we get

(AF)(BD)(CE) =(BF)(CD)(AE) [ AP / BI ][ BP / CK ][ CP / AM ]

which means that we need to only prove that [ AP / BI ][ BP / CK ][ CP / AM ] = 1 to prove our findings.

from equation (3) we can substitute AP / BI with AH / BP and obtain

[ AP / BI ][ BP / CK ][ CP / AM ] = [ AH / BP ][ BP / CK ][ CP / AM ] = (AH)(CP) / (CK)(AM)

To prove (AH)(CP) / (CK)(AM) = 1 is the last step ....................(16)

From our initial constructions we know that AH // CK which makes triangle AHP /// triangle KCP

therefore AH / CK = HP / CP ....................(17)

If we substitute equation (17) into (16) we get

(AH)(CP) / (CK)(AM) = (HP)(CP) / (CP)(AM) = HP / AM

Lastly, because AH // PM and AM // HP from our constructions, quadrilateral AHPM is a parallelogram.

therefore HP = AM because they are the opposite sides of the parallelogram and that makes HP / AM = 1

Q.E.D

Click here to see an extention of this phenomenon,

Back to the first Final Project Page

Back to my Main Page