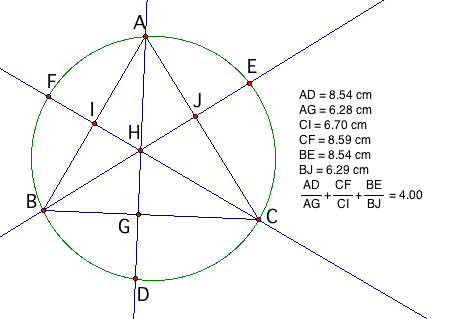
Required to prove: AD/AG+BE/BJ+CF/CI=4 Proof: AD/AG=(AG+GD)/AG=(AG+HG)/AG=1+HG/AG In the same way BE/BJ=1+HJ/BJ and CF/CI=1+HI/CI Now AD/AG+BE/BJ+CF/CI=3+HG/AG+HJ/BJ+HI/CI Now mutliply HG/AG by BC/BC and get 2 area of triangle BHC / 2 area of triangle ABC In the same way get HJ/BJ as 2 area of triangle CHA / 2 area of triangle ABC And HI/CI is 2 area of triangle AHB / 2 area of triangle ABC All the 2's cancel out Now AD/AG+BE/BJ+CF/CI=3+[area of BHC+area of CHA+area of AHB] / area of ABC That is AD/AG+BE/BJ+CF/CI=3+area of triangle ABC / area of triangle ABC = 3 + 1 = 4 Q.E.D.

Back to the Altitudes Page

Back to my Main Page