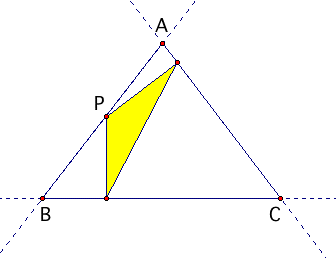
If the point P is on one of the sides of triangle ABC, the point forms one of the vertices of the pedal triangle. The pedal triangle formed with P on one of the sides of triangle ABC will always be on the interior of triangle ABC.

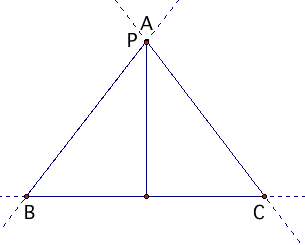
If the point P is moved to a vertex of the original triangle ABC, the pedal triangle "collapses" to just the altitude of the triangle from that vertex.

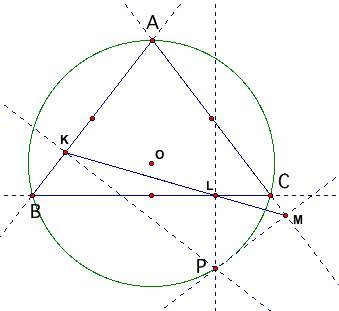
In certain cases the pedal triangle reduces/collapses to three collinear points. The location of P for this to happen is when P is on the circumcircle as indicated alongside. This line is called the Simson Line.

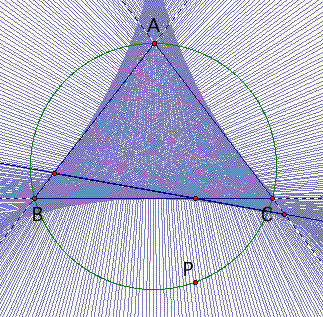
If we trace the Simson Line as the point P moves around the circumcircle, the envelope formed is a deltoid. The area of the deltoid is half the area of the circumcircle.

There are three places where the Simson line forms one of the sides of the original triangle. If P is at point K the Simson Line is side AB, if P is at point L the Simson Line is side BC and if P is at point M the Simson Line is side AC.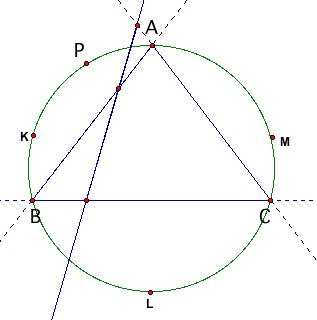

Back to the first Pedal Page

Back to my Main Page