On this webpage, we are going to explore the pedal triangle and various aspects of it. Firstly let us look at the characteristics of a pedal triangle.

The pedal triangle (the yellow triangle alongside) is constructed by dropping perpendiculars from any given point P onto the sides of any triangle ABC. When the points of intersection between the sides of the triangle and the perpendiculars are joined, the pedal triangle is formed. A pedal triangle can be formed from a point P inside or outside of the initial triangle and the pedal triangle can be inside or outside the original triangle.

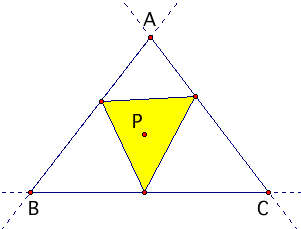Now let us look at four special pedal triangles.

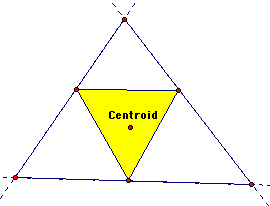The pedal triangle formed by the centroid is always inside the original triangle regardless of the shape of the orignial triangle.

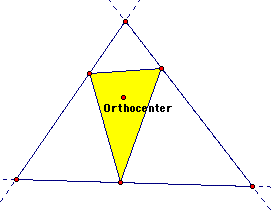The orthocenter is created by the three altitudes of a triangle. From these three altitudes we create the orthic triangle. It is obvious that the pedal triangle created from the orthocenter is the same triangle as the orthic triangle of any triangle. The pedal triangle formed by the orthocenter always stays inside the original triangle regardless of the shape of the orignial triangle.

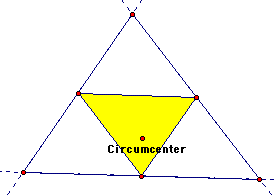Since the circumcenter is constructed from the perpendicular bisectors of the triangle sides, the pedal triangle formed by the circumcenter is also the medial triangle of the main triangle. This will remain so even if the circumcenter is outside the initial triangle. The pedal triangle (just as the medial triangle) is one fourth the area of the initial triangle. The pedal triangle formed by the circumcenter always stays inside the original triangle regardless of the shape of the orignial triangle.

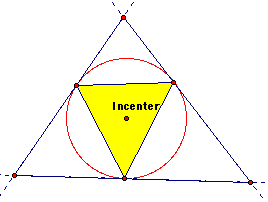Since the incenter is constructed by the angle bisectors of the initial triangle and the pedal triangle is created by dropping perpendiculars to each side of the initial triangle, the pedal triangle produced by the incenter is inscribed by the incircle, as shown alongside. The pedal triangle formed by the incenter always stays inside the original triangle regardless of the shape of the orignial triangle.

For a further exploration of pedal triangles, click here.

Back to my Main Page