The Conics

By: Diana Brown

Day Three:

Some Circle Investigations

What happens to the circumference of a circle if you double the diameter? If you triple the diameter? If you half the diameter? As the diameter increases (or decreases) in measure, how does the circumference change? Why does this change occur?

First we will construct a circle in Geometer’s Sketchpad (GSP):

 

Here are some measurements of the above circle:

Radius: 4.42
Diameter: 8.84
Circumference: 27.76

Now let’s create another circle that has a diameter half the size of the above circle and find the same measurements:

 

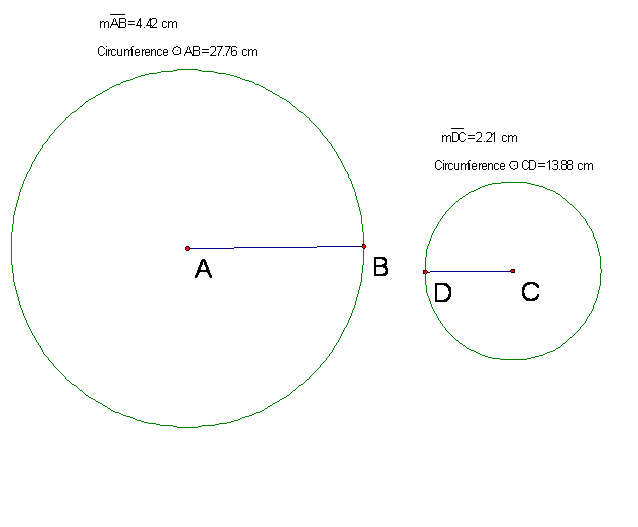
Radius: 2.21
Diameter: 4.42
Circumference: 13.88

Notice that each of the measures (even the Circumference) is exactly one half of the first circle. So as the diameter is halved the circumference is halved.

Why is this so?

Well, what do we know about the circumference of a circle?

The circumference of a circle can be found by multiplying pi (which is equal to 3.14) by the diameter of the circle.

C = πD,

Examples:

Original Diameter = 10

C = π (10) = 31.4

C = π (5) = 15.7

31.4 / 15.7 = 2

Notice that the formula for the Circumference of a circle is a direct variation formula, with Pi being the constant and the diameter and the circumference being the variables. 

What is direct variation?

When two variable quantities have a constant (unchanged) ratio, their relationship is called a direct variation. 
It is said that one variable "varies directly" as the other.  

The constant ratio is called the constant of variation.

  We can show this by circumscribing a square around a circle.

The circumference C of a circle varies directly as the perimeter P of the circumscribed square.

C = k1P

As the boundary of the square changes, the boundary of the circle changes proportionally.

But the perimeter varies directly as the side.  Hence, the circumference varies directly as the side -- because varies directly is a transitive relation:

If a varies directly as b, and b varies directly as c,
then a varies directly as c.

If a = k1b, and b = k2c, then a = k1k2c.

Therefore, the circumference C varies directly as the side s.

But s is equal to the diameter D!

C = kD

 

Suppose a 6-foot tall man is walking around the world. How much further does his head travel than his feet?

 

 

What is the circumference of the earth?

The circumference of the earth at the equator is 24,901.55 miles (40,075.16 kilometers).

But, if you measure the earth through the poles the circumference is a bit shorter - 24,859.82 miles (40,008 km). This earth is a tad wider than it is tall, giving it a slight bulge at the equator. This shape is known as an ellipsoid or more properly, geoid (earth-like).

Information obtained from: http://geography.about.com

Lets use a circumference of is 24,901.55 miles.  If this is so then we can find the diameter by substituting the circumference into the formula:

C = πD,

24,901.55 = πD

Dividing both sides by π gives a diameter of:
D = 7,926.41 miles

To convert this to feet we multiply 7,926.41 miles by 5280 ft/mi = 41,851,442 feet.

Look at the following diagram:

 

 

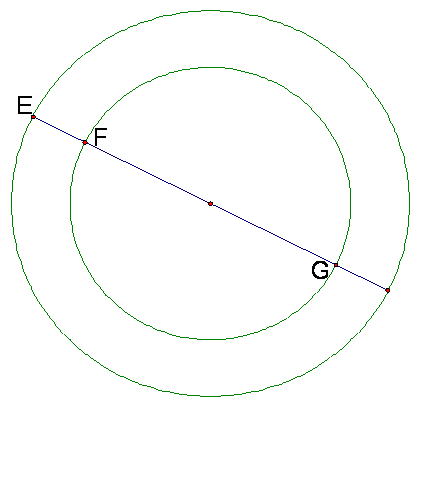
Notice that if FG is the diameter of the earth and the man is the length of EF (F being the point of his feet and E being the point of his head) which is 6 feet tall then we need to add 12 feet to the diameter of the earth to get the circumference that the man’s head is traveling.  Here is how the math goes to determine how much further his head travels than his feet.

 will be the circumference of the earth.  = 24,901.55 x 5280 = 131,480,184 feet.  Which is also the distance the man’s feet travels.

 will be the circumference that the man’s head travels.

 = π (41,851,454) = 131,480,222

To determine how much further his head travels than his feet we will subtract  from :

131,480,222- 131,480,184 = 38 feet.

Other investigations:

1.    When Thomas enters a pizza store, he notices that a 14 inch circular pizza has a price of $7 and a 16 inch circular pizza has a price of $12. He complains the prices are unfair? Why? What should be the "fair" price of the 16 inch pizza?

2.    The trails in a park resemble the following diagram. Find the total length of the trails, given that all the circles have the same area and circle 2 is tangent to the midpoint of L.

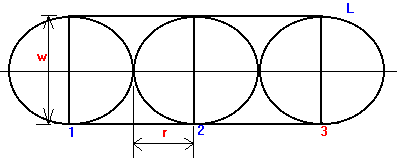
3.    A bicycle wheel has a radius of 13 inches. How many revolutions must the wheel make to go 1 mile?

4.    Suppose a string is wrapped around the Earth at the equator. (Assume the Earth is a sphere with a smooth surface.) Now pretend that we pull the string outward from the earth's surface so that the string is always one-inch away from the earth's surface all the way around the equator. How much more string will be needed to complete this new circle?

 

Return to the Conics Homepage

Return to EMAT 6690 Homepage

Go to Day Four (Ellipse Introduction)