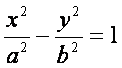The Conics
By: Diana Brown
Day Nine:
Hyperbola Investigations
Definition:
A hyperbola is the set
of all points P such that the difference of the distance from P to two fixed
points, called the foci, is
constant. The line through the foci intersects
the hyperbola at two points, the vertices. The line segment joining the vertices is the transverse axis, and its midpoint is
the center of the hyperbola. A hyperbola
has two branches and two asymptotes. The asymptotes contain the diagonals of a
rectangle centered at the hyperbola’s center.
To get the correct
shape of the hyperbola, we need to find the asymptotes of the hyperbola.
The asymptotes are lines that are approached but not touched or crossed.
These asymptotes are boundaries of the hyperbola. This is one difference
between a hyperbola and a parabola. For the hyperbolas that open
right/left, the asymptotes are:
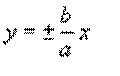
and for hyperbolas
opening up/down, the asymptotes are:
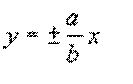
To form the asymptotes
easily on the graph, all we need do is form a rectangle using a and b.
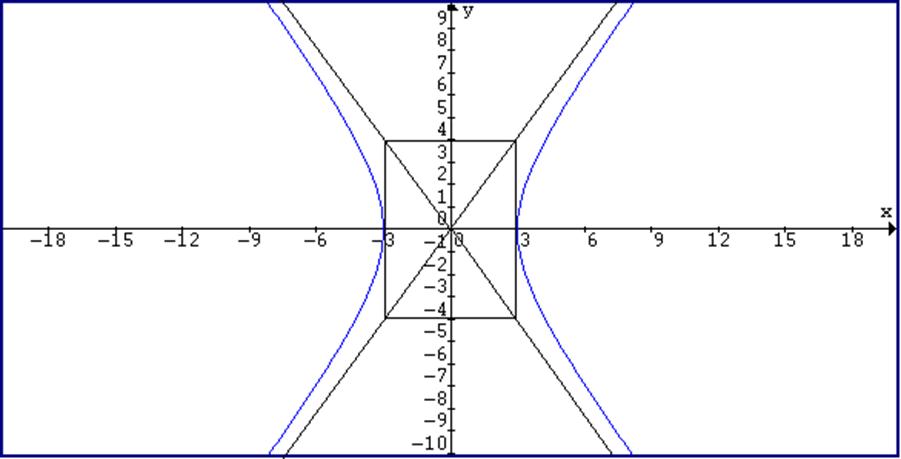
Characteristics
of Hyperbola (center of origin)
|
Equation |
Transverse Axis |
Asymptotes |
Vertices |
|
|
Horizontal |
Y = ±(b/a)x |
(±a, 0) |
|
|
Vertical |
Y = ±(a/b)x |
(0, ±a) |
Foci: c² = a² + b²
Sample
Problems
1.
Draw the hyperbola
given by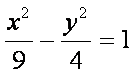 
Solution:
This hyperbola opens right/left because it is
in the form x - y.
a2 = 9, b2 = 4, c2
= 9 + 4 = 13. Therefore, a = 3, b = 2 and c = 3.6.
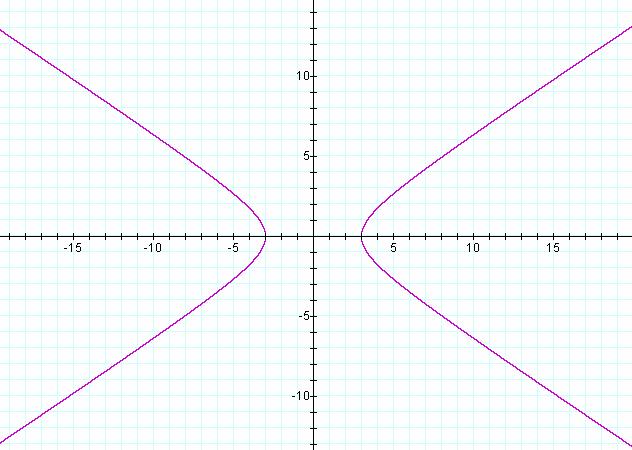
2. Graph the hyperbola
. Find the vertices, foci
and equations of the asymptotic lines.
Solution:
This hyperbola opens right/left because it is
in the form x - y.
a2 = 16, b2 = 4, c2
= 16 + 4 = 20. Therefore, a = 4, b = 2 and c = 4.5
Vertices: (4, 0) and (-4, 0)
Foci: (4.5, 0) and (-4.5, 0)
Equations of asymptotic lines: y = .5x
and y = - .5x
To graph the hyperbola, go 2 units up/down
from center point and 4 units left/right from center point.
3. Write
an equation of the hyperbola with foci at (0, -3) and (0, 3) and vertices at
(0, -2) and (0, 2).
Solution:
Since the vertices and
foci are both y values therefore the hyperbola has a vertical transverse axis,
which means we are working with the equation:
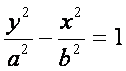
If the vertex is (0,
±2) then a = 2
If the Foci is (0, ±3)
then c = 3
To find b²:
3² = 2² + b²
9 = 4 + b² (subtract
4)
b² = 5
The equation is:
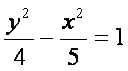
Translations of Hyperbolas
If the hyperbola opens right/left the
translation is:
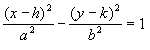
with the equations of the asymptotic lines as:
y - k = + (b/a)(x - h)
If the hyperbola opens up/down the translation
is:
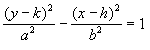
with the equations of the asymptotic lines as:
y - k = + (a/b)(x - h)
Sample
Problems
1. Graph the equation: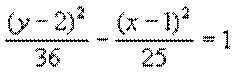 
Find the center, vertices, foci and the equations of the asymptotic lines.
Solution:
Since it is y - x it opens up/down.
a2 = 36, b2 = 25 and
c2 = 36 + 25 = 61.
Thus, a = 6, b = 5 and c = 7.8
Center: (1, 2)
Vertices: (1, 8) and (1, -4) ( six
units up and down from center)
Foci: (1, 9.8) and (1, -5.8) ( 7.8
units up/down from center)
Equations of asymptotic lines: y - 2 = (+6/5)(x
- 1)
The box is formed by going 6 units up/down and 5 units right/left from center.
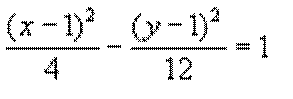
2. Find
the equation of a hyperbola with center (1, 1), vertex (3, 1) and focus at (5,
1).
Solution:
The vertex and foci are on the same horizontal
line.
This makes the hyperbola open
right/left.
a = 2 (distance from vertex to center), c = 4
(distance from focus to center).
Thus a2 = 4, c2 = 16 and
b2 = 16 - 4 = 12.
The equation is:
Hyperbolas
in real life
A hyperbolic mirror
can by used to take panoramic photographs. A camera is pointed toward the
vertex of the mirror and is positioned so that the lens is at one focus of the
mirror.
Return to the Conics Homepage
Return to EMAT 6690 Homepage
Go to Day
Ten (Summary of Conics)