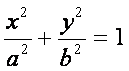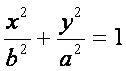The Conics
By: Diana Brown
Day
Five:
Ellipses
Definition:
An ellipse is the set of all
points P such that the sum of the distances between P and two distinct points,
called the foci (±c, 0), is a
constant.
There are two main types of
ellipses: The horizontal major axis
ellipse and the vertical major axis ellipse.
Diagram of a horizontal
major axis ellipse
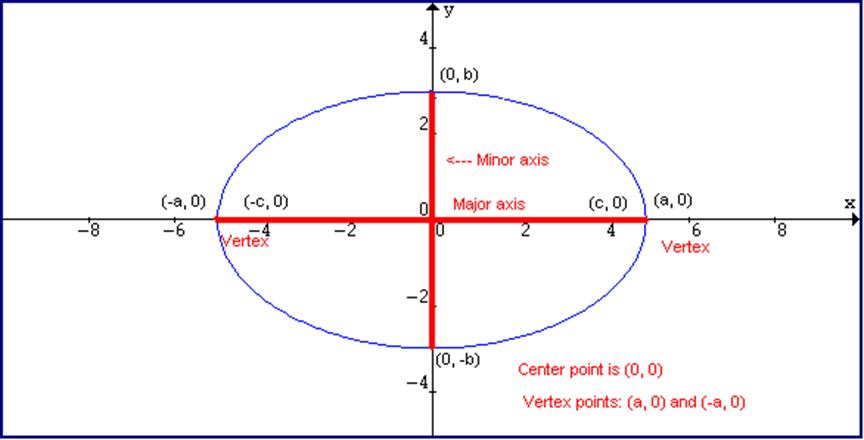
The line through the foci
intersects the ellipse at two points, the vertices. The line segment joining the vertices is the major axis, and its midpoint is the
center of the ellipse. The line
perpendicular to the major axis at the center intersects the ellipse at two
points called the co-vertices (0, ± b). The line segment that joins these points is
the minor axis of the ellipse.
General equation of the
horizontal major axis ellipse:

This ellipse has the major
axis parallel to the x-axis making it open longer across. The length is
2a. The minor axis is parallel to the y-axis and has length 2b. The
foci points are 2c units apart. The center of the ellipse until we
translate it will remain at (0, 0). The vertex points are at the end
points of the major axis. Look at the equation. The a value is always the
biggest number.
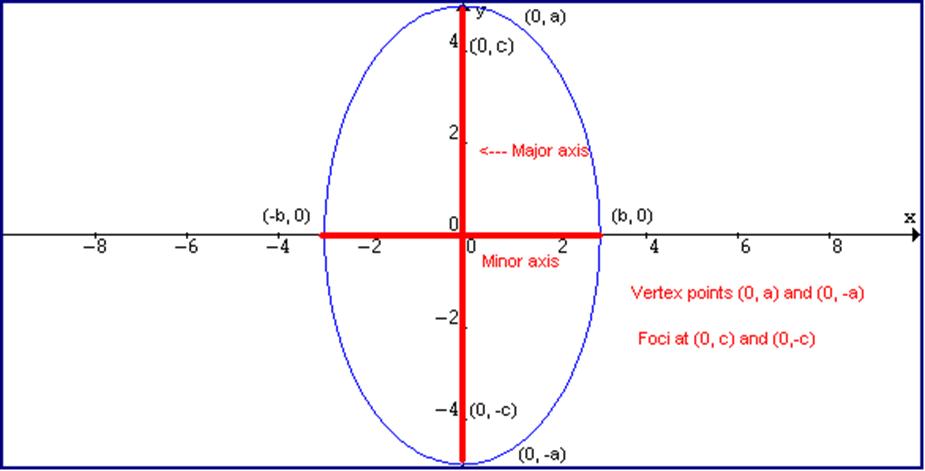
Diagram of a vertical major
axis ellipse
General equation of the
horizontal major axis ellipse:
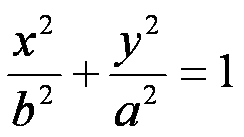
Notice the major axis and
the minor axis have reversed. The longer axis is now vertical. What
causes this to happen? Look at the equation closely. The a value is
now under the y value rather than the x value in the previous diagram. We
now have an easy method to tell which way the ellipse opens. Look to see
whether the larger value is under the x value or the y value.
Summary of the
characteristics of an ellipse (center at origin)
|
Equation |
Major Axis |
Minor Axis |
Co-Vertices |
|
|
Horizontal |
(±a, 0) |
(0, ±b) |
|
|
Vertical |
(0, ±a) |
(±b, 0) |
Equation for the Foci: c² =
a² - b²
Example
Practice Problems
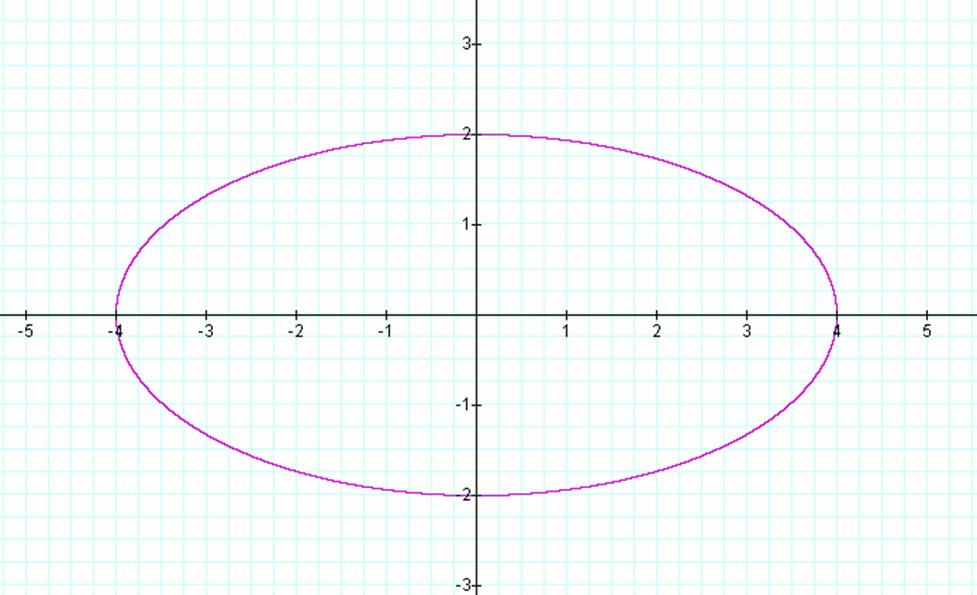
1. Sketch the graph and find the vertices, end
points of the minor axis and foci points for:
x² + 4y² = 16
Solution:
First put the equation in
the correct form by dividing everything by 16:
x²/16 + y²/4 = 1
The larger value is a² = 16
and b² = 4. Since the larger value is under x, the ellipse has a horizontal
major axis.
The values are a = 4, b = 2.
To find c, subtract 16 - 4
and take the square root. Thus c = 3.5
Center at (0, 0)
Vertices: (4, 0) and (-4, 0)
End Co-Vertices: (0, 2) and (0, -2)
Foci: (3.5, 0) and (-3.5, 0)
2. Graph the ellipse given by 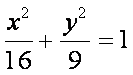 . Identify the center, vertices, co-vertices,
foci.
. Identify the center, vertices, co-vertices,
foci.
Solution:
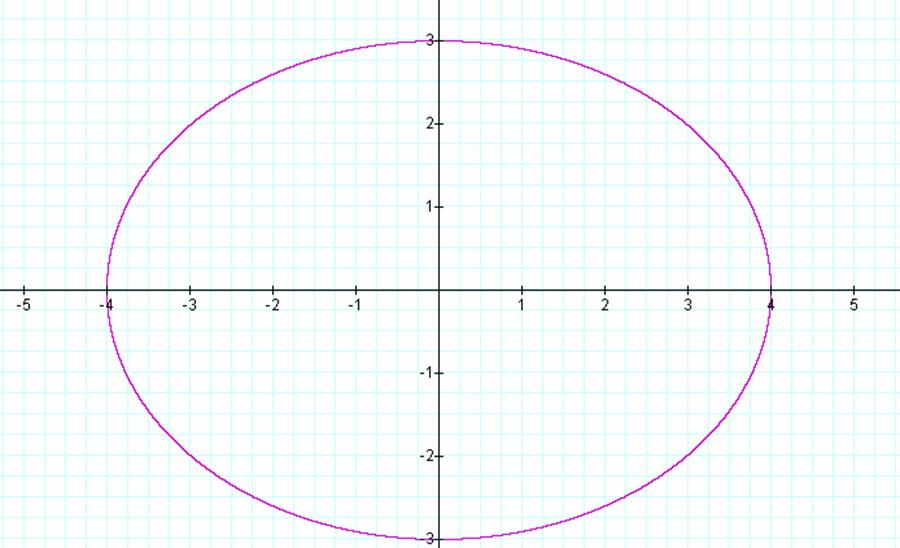
You can see that:
Center: (0, 0)
The ellipse is horizontal
Vertices: (±4, 0)
Co-Vertices: (0, ±3)
a = 4 and b = 3
Major axis: 8 units long
(2a)
Minor axis: 6 units long
(2b)
To find the foci remember to
use the formula: c² = a² - b²
c² = 4² - 3² = 16 – 9 = 7
c = 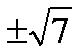
The foci are located at (0, ![]() )
)
3. An ellipse has its center at the
origin. Find an equation of the ellipse with Vertex (8, 0) and minor axis
4 units long.
Solution:
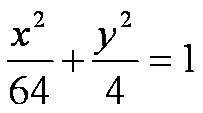
a = 8 and b = 2
The minor axis is 2b = 4, so
b = 2.
The equation is:
4. An ellipse has its center at the
origin. Find an equation of the ellipse with vertex (0, -12) and focus (
0, -4).
Solution:
a = 12 and c = 4.
Both are on the y-axis, so
the major axis is vertical. To find b², square a and c and
subtract.
b² = 144 - 16 = 128
Thus the equation is:
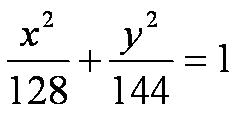
Translation of
the Ellipse

The center is now at (h,
k). All values are now calculated from this point rather than from (0,
0).
Example
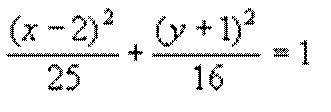
Sketch the graph and find the
vertices, end points of the minor axis and foci for:
Solution:
The larger of the values is
under x. The major axis is horizontal. a = 5, b = 4 and c = 3
Center: (2, -1)
Vertices: (7, -1) and (-3, -1) (add/subtract 5 from the x-value )
End points of minor: (2, 3) and (2, -5) (add/subtract 4 from
y-value)
Foci points: (5, -1) and (-1, -1) (add/subtract 3 from x-value)
Return to the Conics Homepage
Return to EMAT 6690 Homepage
Go to Day
Six