The Pythagorean
Theorem and its many proofs
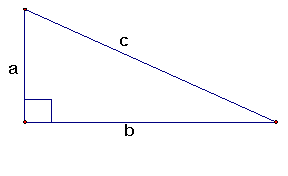
Pythagorean Theorem
In a right triangle, the square of the length of the hypotenuse is equal to the
sum of the squares of the lengths of the legs.
a² + b² = c²
There are several
methods to prove the Pythagorean Theorem. Here are a few:
Method One:
Given triangle ABC,
prove that a² + b² = c².
First construct a
perpendicular from C to segment AB.
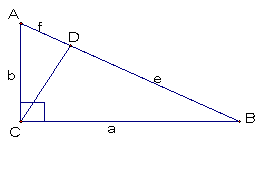
In a right triangle, the altitude from the right angle to the hypotenuse
divides the hypotenuse into two segments (e and f). The length of each leg of the right triangle
is the geometric mean of the lengths of the hypotenuse and the segment of the
hypotenuse that is adjacent to the leg, therefore
![]() and
and ![]() .
.
If I cross multiply
each ratio I get:
![]() and
and ![]()
then adding a and b
yields:
![]() ,
,
factoring out c on the
right side gives:
![]() ,
,
and looking at the above diagram:
![]()
so by substitution we get :
![]()
Method Two:
For this proof I will use the below diagram:

Notice that the area
of the large square could be expressed in two ways:
![]()
or
Summing the area of
the four triangles (![]() ) and the area of the smaller square (
) and the area of the smaller square (![]() ).
).
![]()
Since these both
represent the area of the larger square we will set them equal to one another.
![]() =
= ![]()
Use algebra to
simplify the above equation.
![]() =
= ![]()
If we subtract 2ab
from both sides of the equation we obtain:
![]()
The Pythagorean
Theorem.
Method Three:
For this proof I will
use the below diagram:
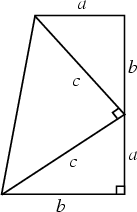
The area
of the above trapezoid can also be expressed in two ways. One is by using the formula for the area of a
trapezoid:
![]()
Let’s use the diagram
above to fill in the formula for the area of a trapezoid:
![]()
The second way to
express the area of the above trapezoid is by summing each geometric figure.
![]()
Since these two
expressions are the area of the above trapezoid we will set them equal to each
other and use algebra to simplify the equation.
![]() =
=![]()
![]() =
=![]()
![]() =
= ![]()
![]() =
= ![]()
Return to Triangle Investigations
Return to my EMAT 6690 Homepage