By: Diana Brown

For any triangle, construct a segment parallel to a base of the triangle that divides the triangle into two equal areas.

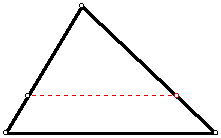
Question: If two similar figures have a ratio K of their areas, what is the ratio of the corresponding sides?

The construction

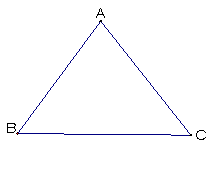
Construct any triangle ABC:

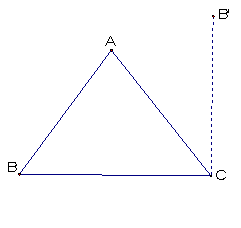
Rotate line segment BC about point C -90 degrees

Construct the line segment B’B and construct its midpoint (point D)

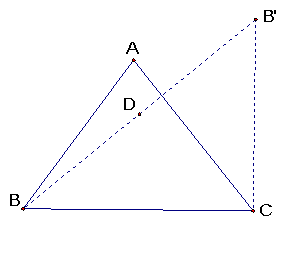
Construct a circle with radius BD with its center at B and mark the intersection of the circle and segment BC (point E)

Construct a line that is through point E and parallel to segment AB and mark the intersection of this line and segment AC (point F)

Construct a line that is through point F and parallel to line segment BC and mark the intersection of this line and segment AB (point G)

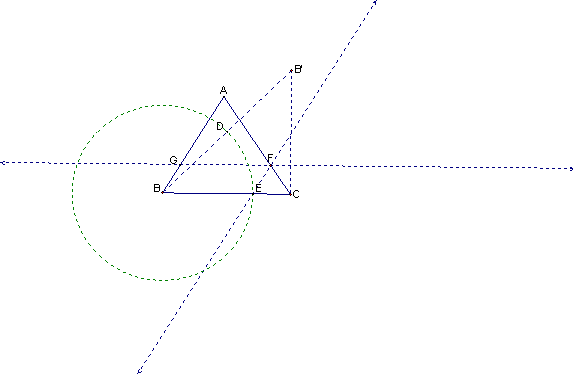
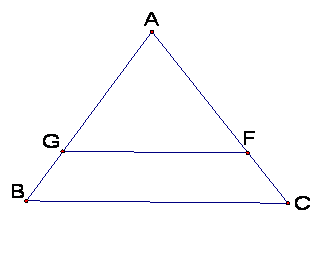
Hide all dashed lines and construct a segment from G to F.

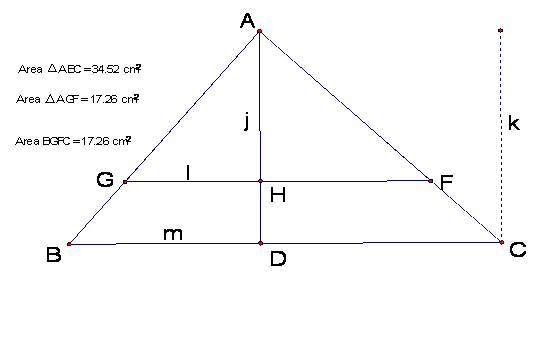
Calculate the area of the triangle AGF and ABC and quadrilateral GFBC. Notice that quadrilateral GFBC and triangle AGF are exactly one half the area of triangle ABC, therefore we have bisected the area of triangle ABC.

Now let’s look at the ratio of the sides:

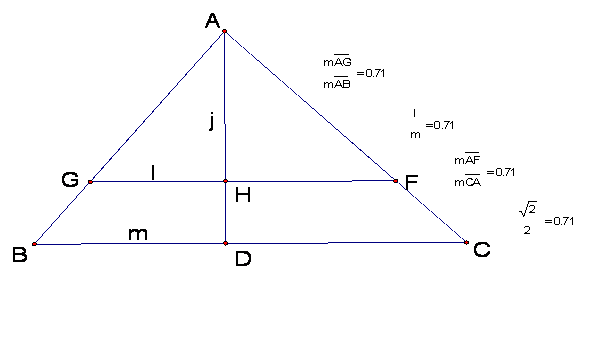
To analyze the ratios of the sides of the triangles lets label a few things and also construct the height of both triangles by constructing a perpendicular line through point A to segment BC.

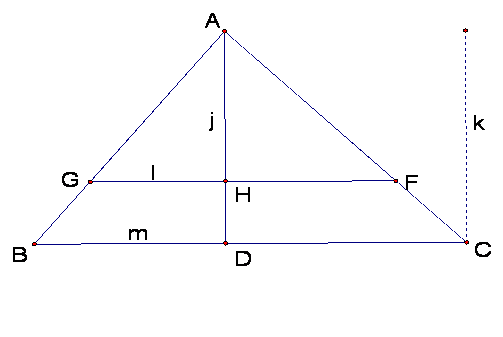
Segment k is the height of triangle ABC and segment j is the height of triangle AGF. Segment l is the base of triangle AGF and segment m is the base of triangle ABC.

First notice that since segment GF is parallel to segment BC then the triangles ABC and AGF are similar.

Because of this we can create the ratios:

The area of triangle ABC = ½ mk

The are of triangle AGF = ½ lj

If we relate these two areas we get:

2lj = mk

By substitution we get

And to solve for l algebraically:

Notice that and if we look at the above diagram we see that the ratio of segments GF and BC are 0.71.

Return to my EMAT 6690 Homepage