Herons Formula

---

Let a,b,c be the sides of a triangle, and let A be the area of the triangle. Heron's formula states that A^2 = s(s-a)(s-b)(s-c), where s = (a+b+c)/2. 
 
Here's one derivation:
 
Consider the general triangle with edge lengths a,b,c shown below: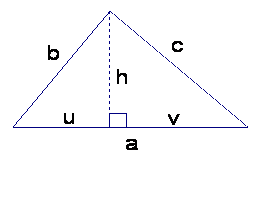
 
 

We have a = u+v, b^2 = h^2+u^2, c^2 = h^2+v^2. Subtracting the second from the third gives u^2-v^2 = b^2-c^2. Dividing both sides by a = u+v, we have u-v = (b^2-c^2)/a. Adding u+v = a to both sides and solving for u gives: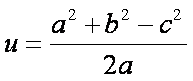
 

 
Taking h = sqrt(b^2-u^2) we have: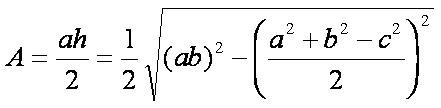
 

 
 
which is equivalent to Heron's formula. Factoring out 1/4, this gives three different ways of expressing (2ab)^2 - (a^2+b^2-c^2)^2 as a difference of two squares. Equivalently, it gives three different factorizations of 16A^2, each of the form
 
 16A^2 = [(a+b)^2 - c^2] [c^2 - (a-b)^2] 
 
Factoring each of these terms gives the explicitly symmetrical form 
 
 16A^2 = (a+b+c)(a+b-c)(c-a+b)(c+a-b) 
 
so if we define s=(a+b+c)/2 we can rewrite the first equation as:
 
 

 
 
 
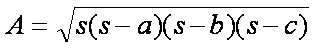
which is the area formula as given by Heron.
 
 
 





Return to Triangle Investigations





Return to My EMAT 6690 Homepage