
Why is a negative number times a negative number a positive
number?
By: Diana Brown
This is a common question by
many students taking mathematics courses in middle school and even high school.† †It is
not surprising to most that this is difficult concept for students to understand.
Negative numbers are not easily understood by most people. †The difficulty with understanding a negative
times a negative is that this is not something we do in our everyday lives. Below
are several methods that may be used to help students better understand
the meaning of a negative times a negative.†
Method One:† Money representations
We can start of explaining
negative multiplication by helping the student understand the easier concepts
such as a positive times a positive or a positive times a negative.† For example in the case of money, we can
represent a positive times a negative by saying $700 is being deducted each
month to pay ones mortgage payment. After six months, how much money has been
taken out of the pay for the mortgage? We can figure out the answer by doing
multiplication.
6 * -$700 = -$4,200.† This is an illustration of a positive times a
negative resulting in a negative.
We can use this same method
to represent a negative times a negative:
Now suppose that, as a bonus,
the employer decides to pay the mortgage for one year. The employer removes the
mortgage deduction from the monthly paychecks. How much money is gained by the
employee in our example? We can represent "removes" by a negative
number and figure out the answer by multiplying.
-12 * -$700 = $8,400
This is an illustration of a
negative times a negative resulting in a positive. If one thinks of
multiplication as grouping, then we have made a positive group by taking away a
negative number twelve times.
Method
Two:† A mathematical illustration
Most students are quick to agree that a negative number can be represented as a
number times -1.† The illustration of a negative times a positive is easier to understand.† So if we take a number and multiply the
number times -1 it is represented below:
†
(-1)x = -x.† Two negative
numbers being multiplied together can be represented as followed:
(-x)
(-y) = (-1) (x) (-1) (y) = (-1) (-1) (x) (y), So what is (-1)(-1)?
First
we will start with things that we know.†
For example, we know that -1(0) = 0.
We
can rewrite (-1)(0) = (-1)(-1 + 1), then using the
distributive property on the right side of the equation we get:
(-1)
(-1) + (-1) (1)
Now
we know that (-1)(1) = -1, but we arenít sure what (-1)(-1) is, but we do know
that whatever it is must be the equation is equal to zero, so since it canít be
-1 for that would make the equation equal to -2, then it must be +1. See the
math below:
0 = (-1) (0) = (-1)(-1 + 1) = (-1) (-1) + (-1) (1) = ? + (-1) therefore
0
= ? + (-1), from our statement above (-1)(-1) must be +1 to complete the statement: 0 = ? + (-1).† Which may
help to conclude that a negative times a negative equals a positive.
Method
Three:† A proof
Let a and b be any
two real numbers. Consider the number x defined by
x = ab + (-a)(b) + (-a)(-b).
We can write
x = ab + (-a)[ (b) + (-b) ]†††††† (factor out -a)† = ab + (-a)(0)† = ab + 0† = ab.
Also,
x = [ a + (-a) ]b + (-a)(-b)††††† (factor out b)† = 0 * b + (-a)(-b)† = 0 + (-a)(-b)† = (-a)(-b).
So we have
x = ab
and
x = (-a)(-b)
Hence, by the transitivity of equality, we have
ab = (-a)(-b).
Method
Four:† Using words to represent negative
numbers
Some
people think of the word ďNOTĒ as a negative meaning.† One might say I am NOT going to my friendís
house.† This seems like a negative version
of saying I AM going to my friendís house.†
So what if I said this with two NOTS.†
I am not going to not go to my friendís house.† It seems the two NOTS cancel each other out
and I am going to my friends house is derived.†
This seems that a double negative statement really derives a positive
statement.† More examples:
|
Negative * Negative |
Positive |
|
He cannot just do
nothing |
He must do something |
|
a not infrequent visitor |
a frequent visitor |
|
I don't never go |
I go |
Method
Five:† Pattern recognition
Lets look at the sequence below.† Notice what happens to the right side of the
equation as the first number goes down by one:
4
x 5 = 20
3
x 5 = 15
2
x 5 = 10
1
x 5 = 5
0
x 5 = 0††††††††††††††††††††††† We notice that the numbers are going down by 5.† Lets keep going:
-1
x 5 = -5
-2
x 5 = -10
-3
x 5 = -15
-4
x 5 = -20. †††††††††††††††† Now lets do this same kind of sequence replacing 5 with -5.
4
x -5 = -20
3
x -5 = -15
2
x -5 = -10
1
x -5 = -5
0
x -5 = 0††††††††††††††††††††† We notice that the numbers are going up by 5.† If we use the same logic as before then we
will see that:
-1
x -5 = 5
-2
x -5 = 10
-3
x -5 = 15
-4
x -5 = 20. †††††††††††††††† Therefore it
seems that a negative times a negative is again a
positive.
Method
Six: Using technology
We
can use the coordinate system in Geometerís Sketchpad to create a line.
Remember that the slope of a line is rise over run.† If we plot a point in the coordinate plane
and use a slope to plot a second point we will look at the slope to determine
if the line has a positive slope of a negative slope.†
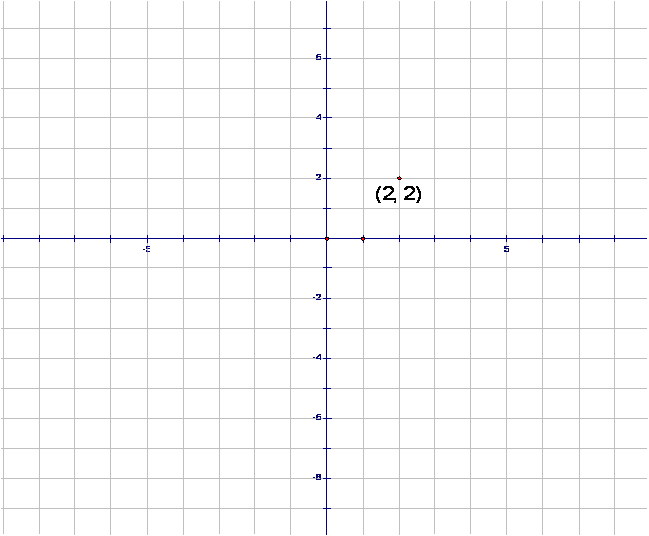
In
the following diagram we plotted a point (2, 2):
Letís
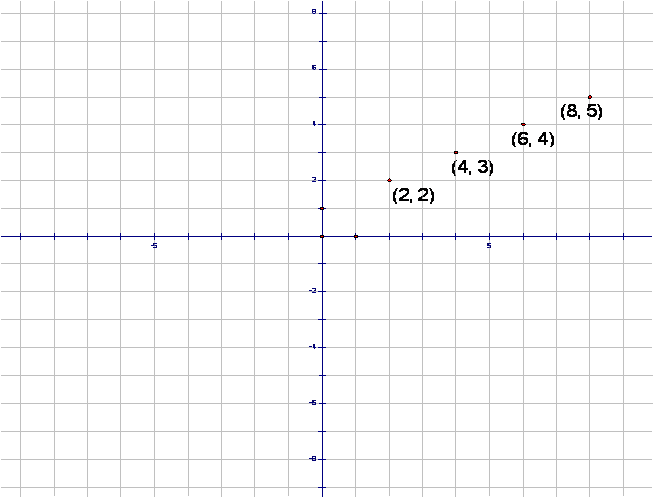
use a slope of 1/2 to find the next three points.
Now
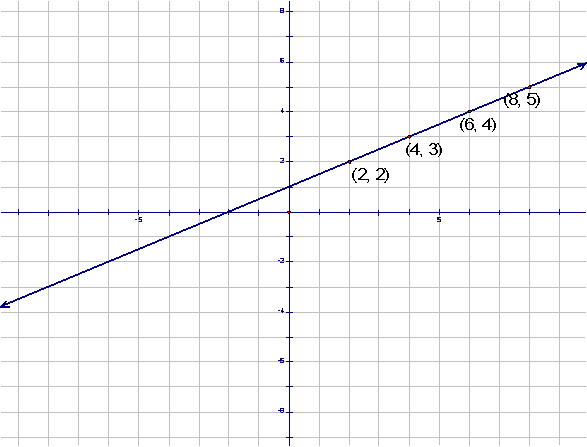
if we construct a line through the points we will see that the result is a line
with a positive slope.
Letís
try this same thing starting at the point (2, 2) and using the slope -1/-2.† See the diagram below for results.
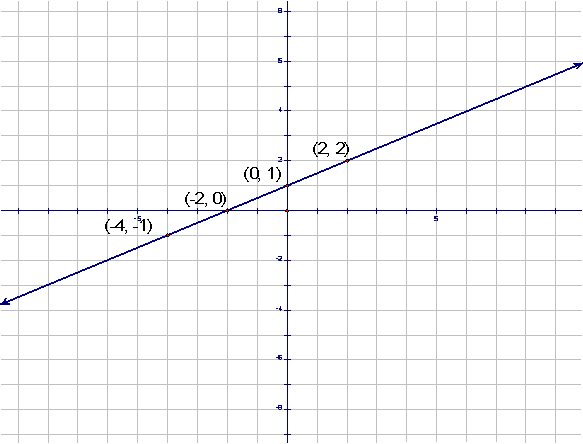
Notice
that the line is the same as before, a positive slope.† Therefore this could be a graphical approach
to showing the relationship of two negative numbers.
Websites
used to help the discovery of different methods:
www.mathforum.org
plato.stanford.edu