
Tangent Circles
By: Diana Brown
Given
two circles and a point on one of the circles, construct a circle tangent to
the two circles with one point of tangency being the designated point.
Steps to creating a circle tangent
to the two circles:
Draw two circles with the smaller
circle being completely inside the larger circle
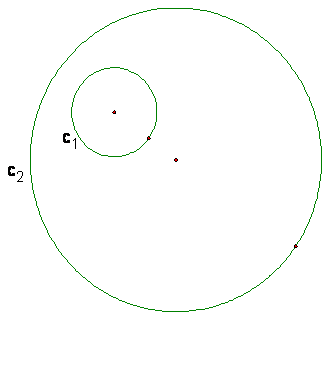
Construct a point on the larger
circle by selecting the larger circle and go to construct point on circle.† Then construct a line from the center of the
larger circle to this point.
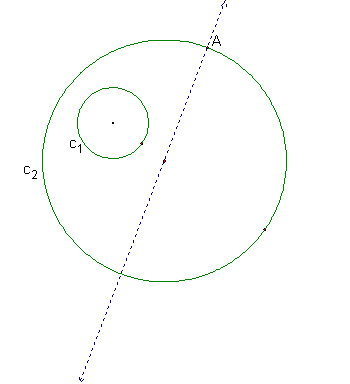
Lets create a copy of the smaller
circle with its center on the point of the larger circle created in step
2.† We can do this by selecting the
radius of the smaller circle and the point on the larger circle and then go to
construct and select circle by center + radius.

Construct a line segment from the
center of the smaller circle to the intersection of the copied circle with the
dashed line from the center, and construct its perpendicular bisector.
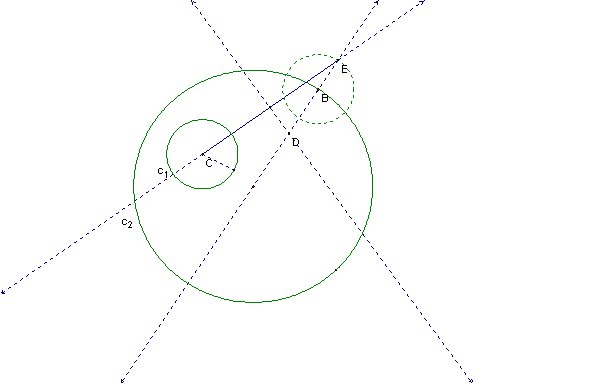
If we connect the intersection of
the lines with the center of the smaller circle, we get an isosceles triangle. You
can also see that the intersection of the lines is equidistant from the
original circles. This distance is what we will use for the radius of the
tangent circle.

Letís hide all of the dashed items
to get a clear view of the two original circles and their tangent circle.
Click on the directly above
picture for a script tool for tangent circles.
Letís explore what happens if we
trace the center of the tangent circle while animating the point on the larger
circle about the larger circle.

An ellipse is created.
Lets explore what happens if we do
the same traces as above but we move the smaller circle to the outside of the
larger circle.
The traces now create a hyperbola.
Click on the above picture to do
your own explorations.

