
Pedal Triangles
By: Diana Brown
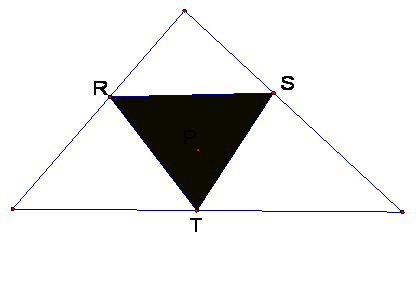
1a. Let triangle ABC be any
triangle. Then if P is any point in the plane, then the triangle formed by
constructing perpendiculars to the sides of ABC (extended if necessary) locate three
points R, S, and T that are the intersections. Triangle RST is the Pedal
Triangle for
1b. Click here
for a script tool for the general construction of a pedal triangle to triangle
ABC where P is any point in the plane of ABC.
2. What if pedal point P is the
centroid of triangle ABC?
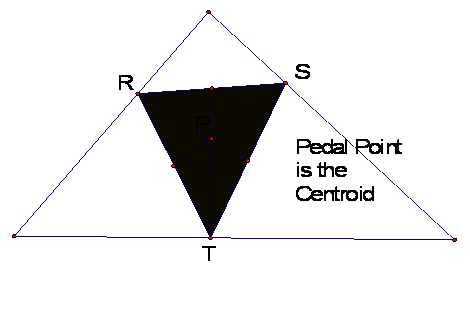
The Pedal Triangle is inside
triangle ABC and the Pedal point is
inside both triangles when P is the centroid.
3. What if . . . P is the Incenter
. . . ?
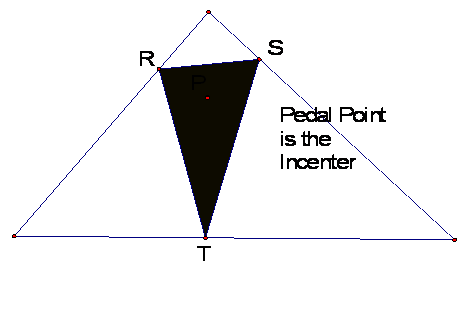
The Pedal Triangle is another
acute triangle that is inside triangle ABC when P is the Incenter.
4. What if . . . P is the
Orthocenter . . . ? Even if outside ABC?
Inside ABC:

The Pedal Triangle stays in side
triangle ABC and the pedal point is inside both triangles ABC and RST
Outside ABC:

The Pedal Triangle overlaps
triangle ABC and the Pedal Point is outside both triangles ABC and RST.
5. What if . . . P is the
Circumcenter . . . ? Even if outside ABC?
The Pedal Triangle is inside triangle
ABC when the pedal point is inside triangle ABC.
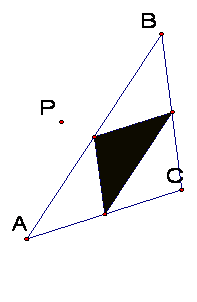
The Pedal Triangle is inside
triangle ABC even when the pedal point is outside triangle ABC.
6. What if P is on a side of the
triangle?
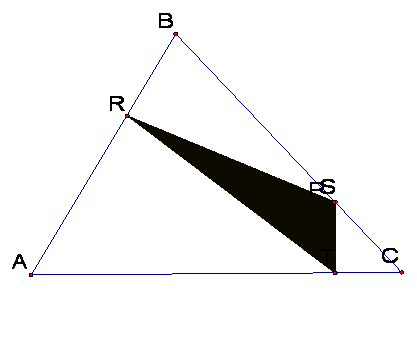
If you drag the pedal point to one
side of triangle ABC it becomes one of the vertices of triangle RST. The pedal
triangle also always stays inside triangle ABC.
7. What if P is one of the
vertices of triangle ABC?
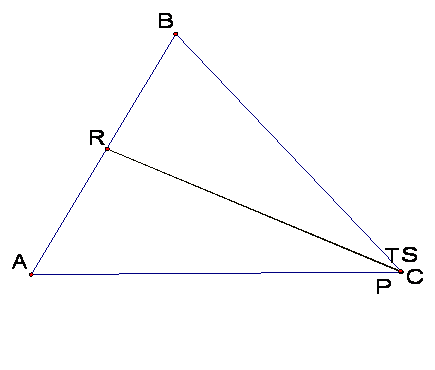
If we take the pedal point to one
of the vertices of triangle ABC the pedal triangle RST degenerates. Thus the points of the pedal triangle are
collinear.
Click here
for the pedal triangle GSP file to do explorations of your own.