---

Exploring Parametric Curves

By: Diana Brown

---

A parametric curve in the plane is a pair of functions

where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t.

---

EXPLORATIONS:

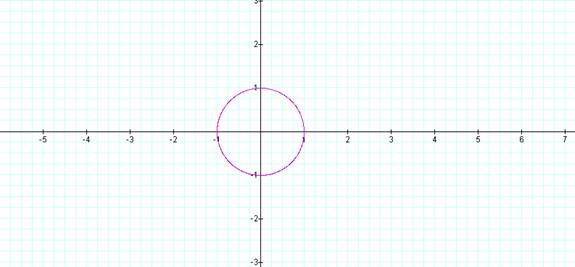
Graph

x = cos (t)

y = sin (t)

for 0≤ t ≤ 30

How would you change the equations to explore other graphs?

For example: for various a and b of the graphs:

x = cos (at)

y = sin (bt)

for 0 ≤ t ≤ 30

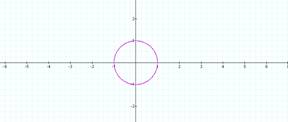
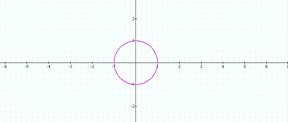
First lets investigate different values of a and b, but keeping a = b.

a=2=b a=3=b

a=4=b a=10=b

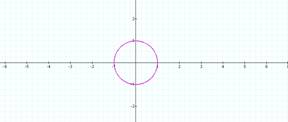
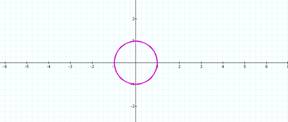
All circles.

Now lets investigate when a = 1 and b varies

b = ½ b = 2

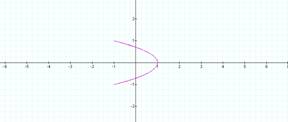
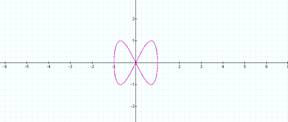
b = 3 b = 4

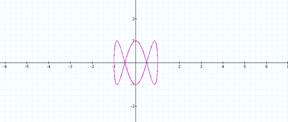
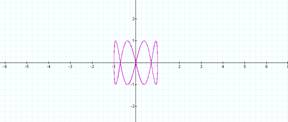
Notice that when a = 1, b determines the number of loops

Now lets investigate when a = ½ and b varies

b = 1 b = 2

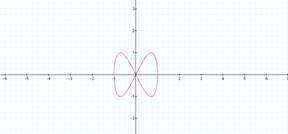
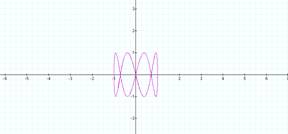
This pair creates two loops This pair creates 4 loops

b = 3 b = 4

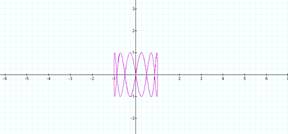
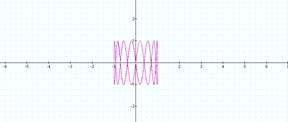
This pair creates 6 loops This pair creates 8 loops

Notice that when a = ½ then the number of loops is determined by 2b.

Now lets investigate when a = 2 and b varies

b = ½ b = 1

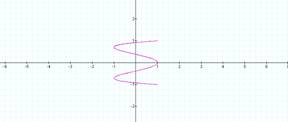
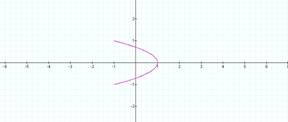
b = 3 b = 4

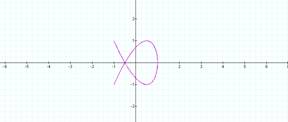
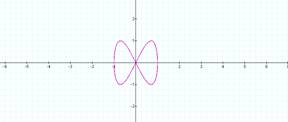
It now seems as though the number of loops is determined by ½b, let’s try two more to see what happens:

b = 5 b = 6

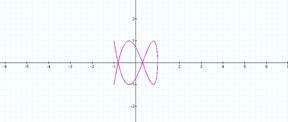
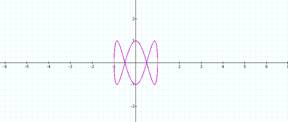
It seems to be so.

Now lets hold b to be constant and vary a. For the following graphs b =1.

a = ½ a = 2

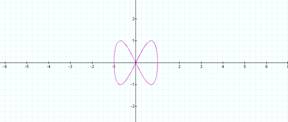
a = 3 a = 4

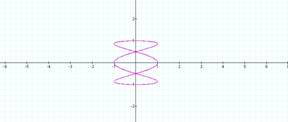
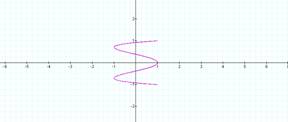
It seems to do the same as above except about the y axis and when a is even it is open curves. Let’s try two more to see if this is true.

a = 5 a = 6

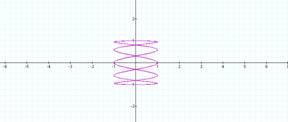
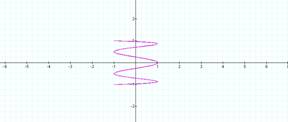
It looks as though we will get something similar about the y axis when b is held constant and a is changing, just as the curves were changing above when a was held constant and b was changing.

---

Return to Homepage

---