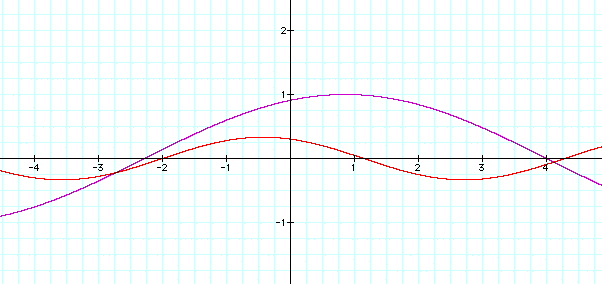
First, I will begin this exploration by looking at positive values of a.
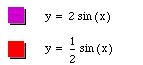
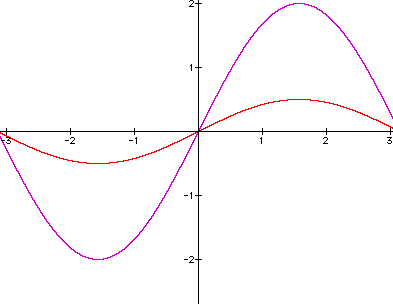
As you can see, when a=2 this increases the maximum of the sin (x) curve to 2. When a=1/2 this decreases the maximum of the sin (x) curve to 1/2. So the a term only effects the amplitude of the sin curve. The amplitude of y= sin x is half the distance between the maximum and minimum values of the function or |a|.
When a is negative.....
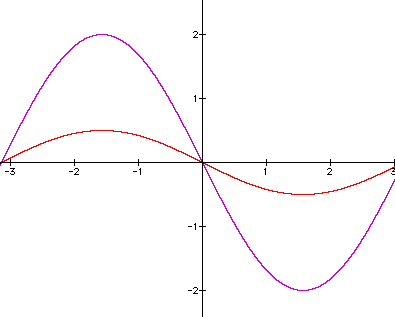
When a are negative values then the sin curve is reflected over the axes.
Now we will look at positive values of b
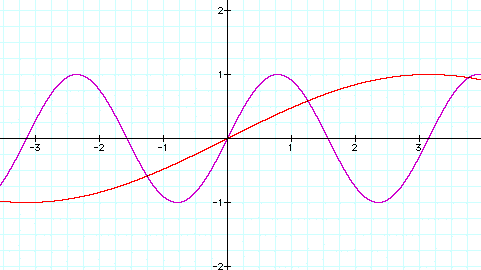
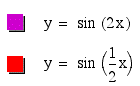
When b=2, this shortens the period of the function and when b=1/2 this lengthens the period. The formula for the period is given by 2pi/b.
When b is negative.....
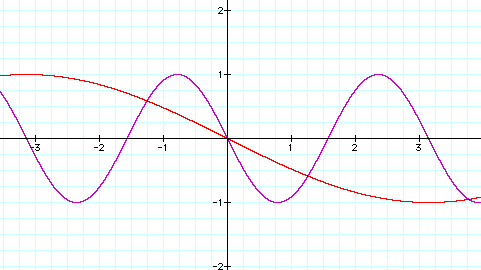
In regards to the length of the period, the negative values of b act the same as the positive values. They shorten the period if b is greater than one and lengthen the period if b is less than. The negative value does change the graph in the respect that it reflects the positive graph over the axes.
Now lets look at values for c
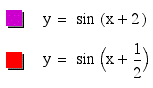
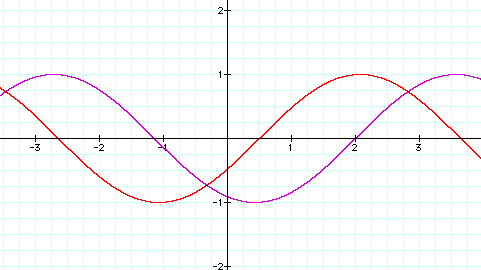
As you can see, the graph does not pass through the origin like the our other graphs. The c term changes the where the period starts. When c=2 the period starts at -2 and when c=1/2 the period starts at -1/2.
When c is negative....
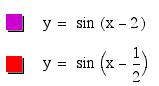
When c=-2 the period starts at 2 and when c=-1/2 the period starts at 1/2.
When all of the values are changed you can get very interesting graphs. Here are some examples!!!