

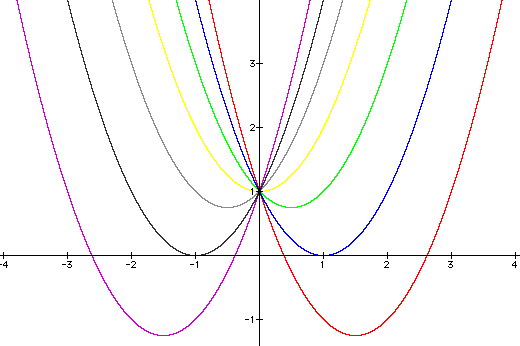
As you can see geometrically, the b-value changes the position of the vertex. All of the graphs have different vertices but they all pass through the point (0,1). We can see from the graph that when b<-2 or b>2, then we have two real roots (or where the graph crosses the x-axis). When b=-2 or 2, there is only one root. When -2<b<2 then there are no real roots because these graphs never cross the x-axis.
Now lets consider the locus of the vertices of the set of the parabolas graphed from
What happens if we connect the locus of the parabolas??

This formula was choose because all of the graphs have this formula in common except for the a coefficient is negative which as you can see means that the graph will be concave downward.
Lets consider other planes....
By revising our original formula we can get different planes. For example if we vary b and x but the other coefficients are fixed then we will get a formulas for the xb-plane. Lets look at the xb-plane!
XB-Plane
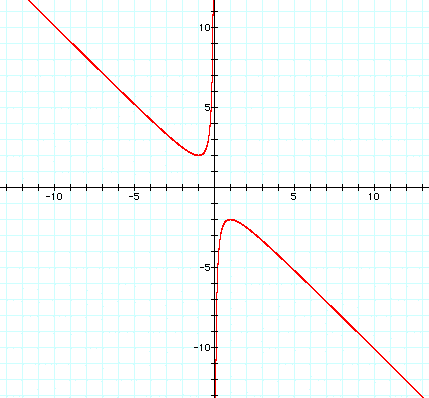
By looking at this equation we are assigning the y-axis to be the b-axis. In this graph the b-axis becomes an asymptote for the graph. This can be very helpful for learning how the b coeffient effects the quadratic function. This process can also be repeated for the other coeffients a and c.