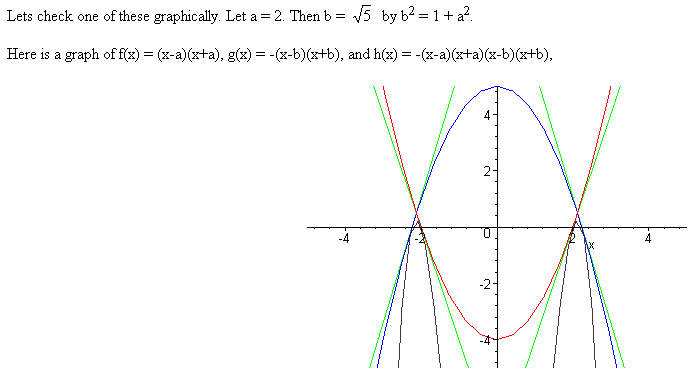It looks promising as we now appear to have g(x) and h(x) tangent at two points. Perhaps a shift in f(x) will create two tangents there. Let's try f(x) = x²-1.

That is not any better. Experiment with the vertical shifts, and you should discover f(x) = x²-1 and g(x) = x²+2.

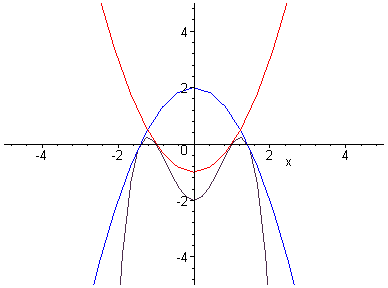
It looks like success!  Let's Prove it.

f '(x) = 2x, g'(x) = -2x, and h'(x) = (fg)'(x) =2x(-x²+2)-2x(x²-1) = -4x³+6x. We'll need these to find the slopes of the tangent lines.

Here is a picture of f(x), g(x), h(x), and the tangent lines.

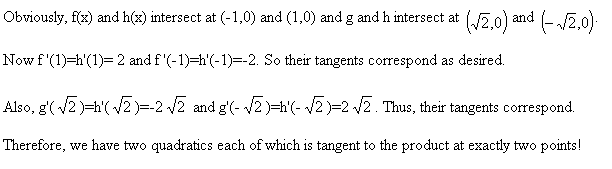
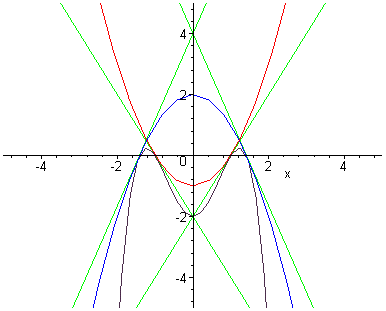
Inspired by this success and some intuition gained from the graphs, lets see if we can algebraically find a family of solutions.

If we let f(x) = (x-a)(x+a) and g(x) = -(x-b)(x+b), then h(x) = -(x-a)(x+a)(x-b)(x+b), and we are guaranteed that f and g will always intersect h at (a,0), (-a,0) and (b,0), (-b,0) respectively. Thus we need only find a and b such that f '(a) = h'(a) and g'(b) = h'(b). This is actually easier than it seems.

Since f(x) = x² - a² , g(x) = x² - b², and h(x) = -x⁴ + (a²+b²)x² + a²b²,

f '(x) = 2x, g'(x) = -2x, and h'(x) = -4x³ + 2xa² +2b²x.

A little algebra with f '(a) = h'(a) gives, ab²-a³-a=0 and, ba²-b³-b=0 from g'(b)=h'(b).

If we assume that a and b are nonzero, we get the hyperbolas b² - a² = 1 and a² - b² = 1.