Tom Cooper

If we rotate a point (a,b) about the origin by degrees, then equations relating it to its image are

x = a cos() + b sin()

y = -a sin() + b cos()

Let’s apply this with = 45^o to x² + nxy + y² = 9.

x² + nxy + y² = 9

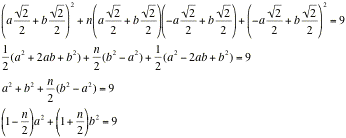
Now we can see that this is an ellipse centered at the origin for –2<n<2.

It is a circle of radius 3, centered at (0,0), when n = 2, and it is a hyperbola centered at the origin when n<-2 or n>2.