Assignment 3: Exploring Coefficients and Roots

by

Tom Cooper

Let's explore how viewing an equation in a plane other than the regular xy plane reveals information about its roots.

We will begin by examining y = x² + bx + 1.  What happens as we vary the values of b?

The following animation shows the graph as b runs from -5 to 5 with 100 steps. The moving parabola is y = x² + bx + 1 and the other parabola is y = -x² + 1.

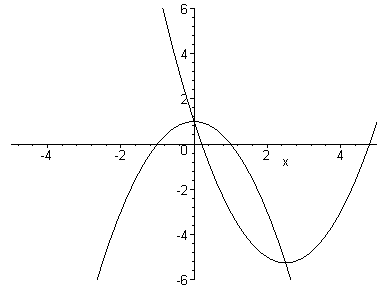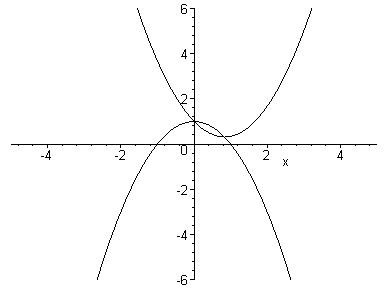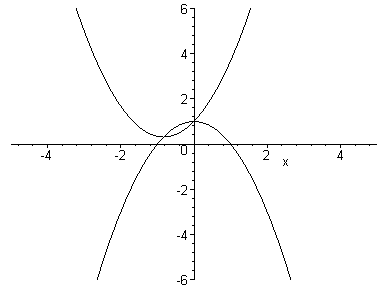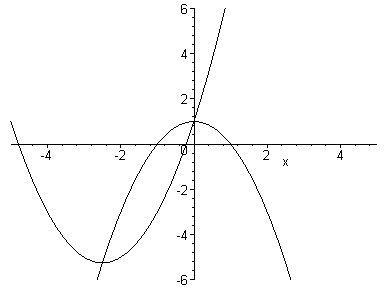
It appears that as b varies, the graph of y = x² + bx + 1 is translated along y = -x² + 1.

In fact this will generalize to varying b in y = ax² + bx + c causes translations along y = -ax² + c. Why?

How do the types of roots change with b? Instead of animation, let's look at several plots together.

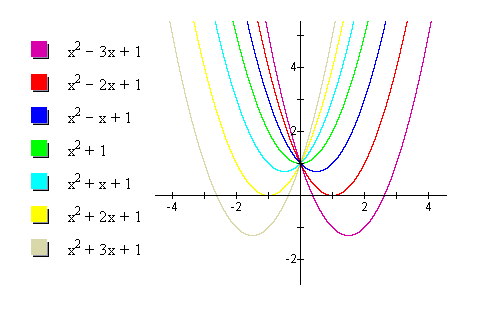
One thing that we can observe from the above graph is that y = x² + bx + 1 = 0 has 2 (real) positive roots when b<-2, 1 (real) positive roots when b = -2, no real roots when -2<b<2, 1 (real) negative root when b = 2, and 2 (real) negative roots when b>2.

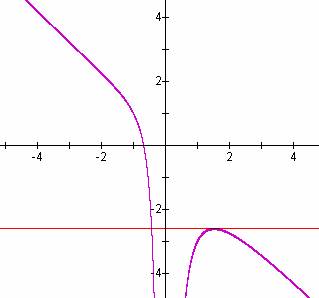
Another way to see this would be to graph the equation in the xb plane. In order to do this, we will plot x² + yx + 1 = 0, since our software likes to use the xy plane.

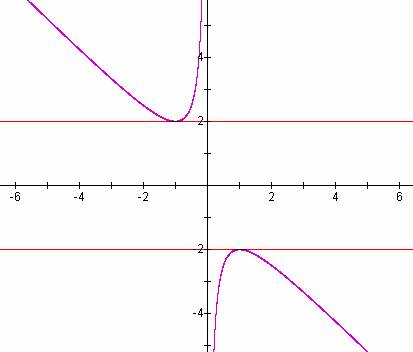
The purple graph is x² + bx + 1 = 0. Since all points on the purple graph satisfy x² + bx + 1 = 0 (i.e., they are roots), the intersections with b = k give the roots when b is a given value k. So this graph also shows that  y = x² + bx + 1 = 0 has 2 (real) positive roots when b<-2, 1 (real) positive roots when b = -2, no real roots when -2<b<2, 1 (real) negative root when b = 2, and 2 (real) negative roots when b>2.

Here is a plot that animates the curve and shows the correspondence in the xb plane. The parabola is y = x² + bx + 1.

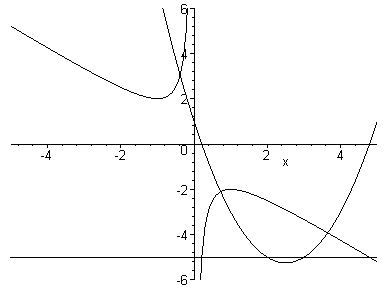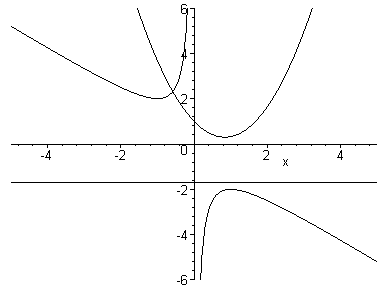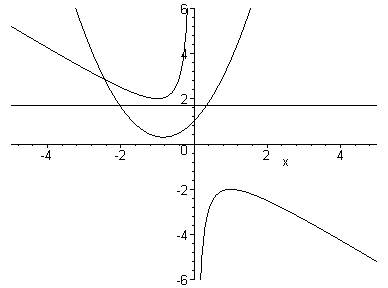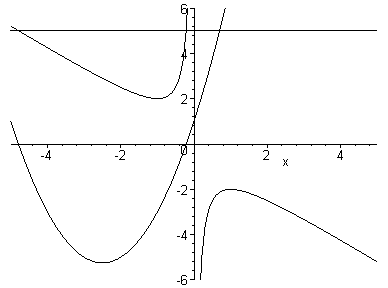
Of course we could fix any two of the coefficients and observe the behavior of the roots upon varying the third.

Instead, let's look at a similar procedure with a cubic equation, y = x³ + bx² + x + 1 = 0.

Here is an animation as b varies from -5 to 5.

Now here is the animation combined with x³ + bx² + x + 1 = 0 in the xb plane.

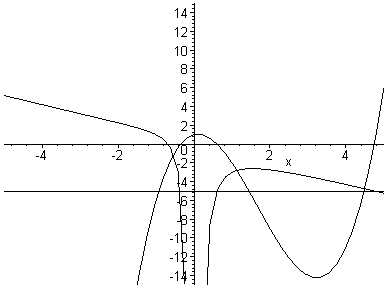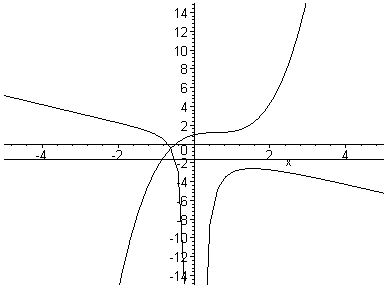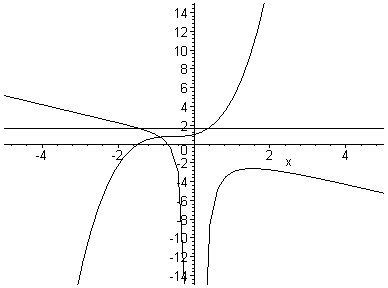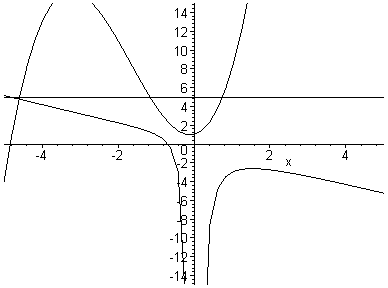
It appears that the function will have 3 real roots (2 positive, 1 negative) when b < -2.6 (approximately), 2 real roots (1 positive, 1 negative) when b = -2.6, and 1 real negative root when b > -2.6