
Assignment 6: Constructing Triangles
by
Tom Cooper
In this assignment, we will explore the idea of constructing a triangle whose sides are the medians of a given triangle and the reverse construction.
First, let's see if we can construct a triangle given three segments. We can begin by making a copy of the first segment. I have chosen to do this by making a circle with this radius and marking off a radius.

Now at one end of our base segment construct a circle with radius equal to the length of the second segment, and construct a circle with radius equal to the length of the third at the other endpoint.
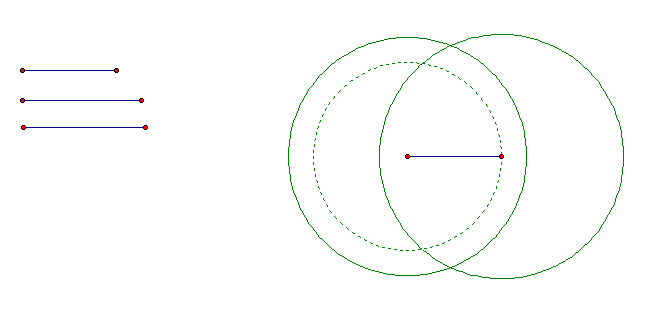
Now any segment from the left endpoint to the circle centered there will have the same length as the second segment, and any segment from the right endpoint to the circle centered there will have the length of the third segment. So to complete a triangle, just make segments from the endpoints to the intersection of these two circles.
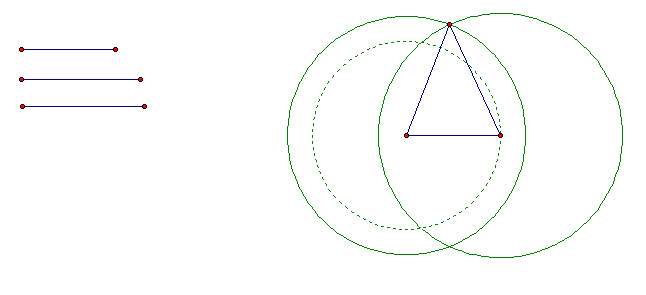
Click here to explore this construction in GSP.
Now we are ready to tackle the following problem: Given a triangle ABC, construct a triangle whose sides are equal to the medians of triangle ABC.
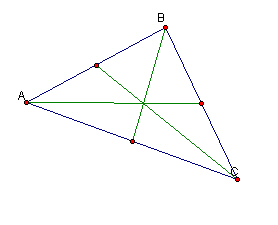
We can use the same construction technique as before, letting the medians be our three segments.
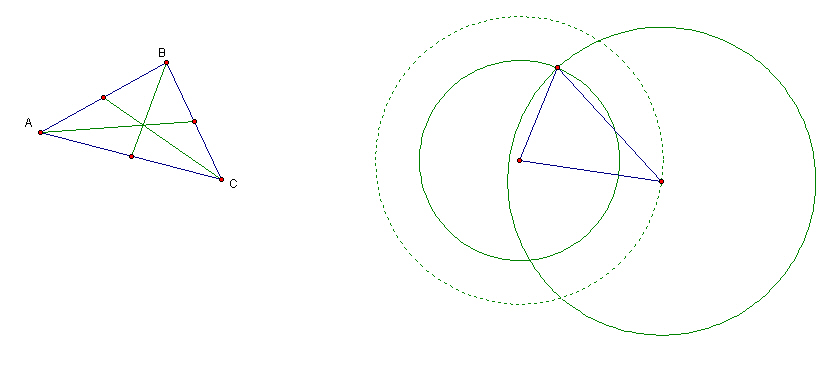
Geometer Sketchpad allows us to explore relationships such as area ratios very easily.
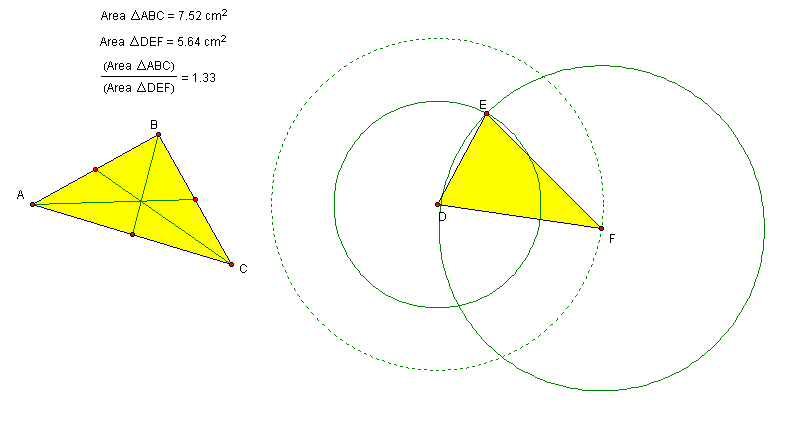
It appears that the original triangle's area is four-thirds the area of the triangle constructed from the medians. Can you prove this? Explore it here.
Now suppose that instead of starting our new triangle by making a copy of a median, we work off of an existing median.
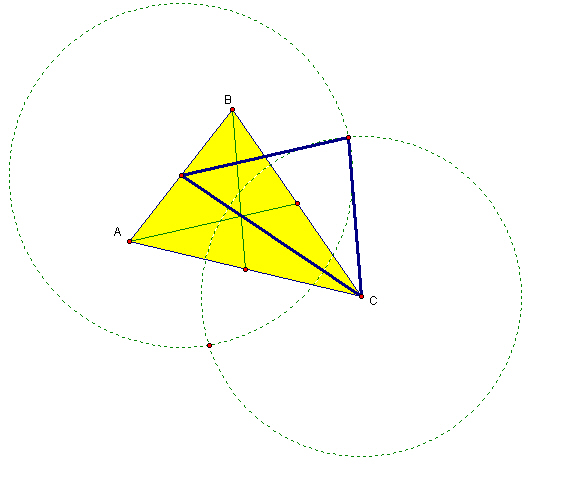
It is very convincing in GSP that the sides of the new triangle are parallel to the original medians. Can you prove this?
Using this construction, we can go backwards. Given three segments, we can construct a triangle with these sides. We can then reverse the above construction to obtain a triangle whose medians are the same length as the original segments.
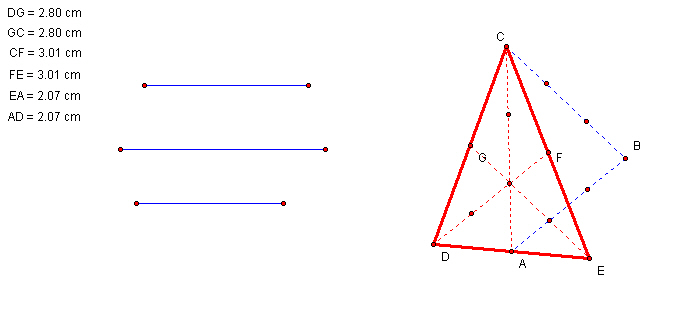
To do this construction, I used the fact that the original medians can be placed parallel to the ones in the triangle of medians, and I used the fact that the medians intersect at a point two thirds of the way from the base to the vertex. This required a segment trisecting tool. Here is a picture without hiding some of the construction lines.
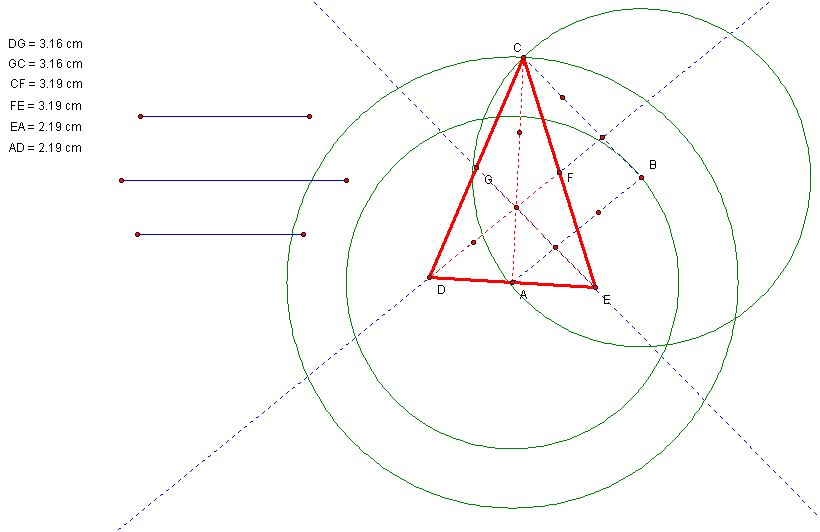
Click here for the GSP file.