
Assignment 8: Orthocenters and Circumcenters
by
Tom Cooper
This assignment asks us to look at the orthocenter of a triangle and explore relationships with new triangles formed with it.
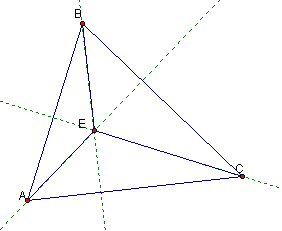
First we will see that if we form a new triangle by replacing one of the vertices A, B, or C by the orthocenter E, the new triangle with have the excluded vertex as its orthocenter.
Let's consider triangle AEC. Since the original altitude from B to AC is perpendicular to AC and passes through E, it is the altitude of triangle AEC from vertex E.
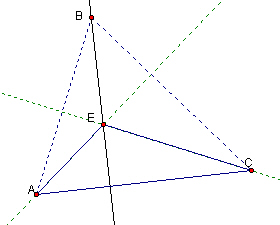
The altitude from A must pass through A and be perpendicular to the line containing EC. Since EC is an altitude of triangle ABC, the line containing AB is perpendicular to the line EC and is therefore the altitude from A in triangle AEC.
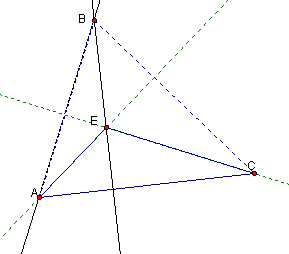
Since we have a theorem that the three altitudes intersect at a single point, it is enough to find the intersection of two of them to locate the orthocenter. So the orthocenter of triangle AEC is the intersection of the line containing AB and the line containing EB, which is precisely B. A similar argument will work for triangles AEB and BEC.
Now consider the following construction. Create a triangle ABC and find its orthocenter E. Construct the triangles AEC, AEB, and BEC. Now construct the circumcircles of triangles ABC, AEC, AEB, and BEC.
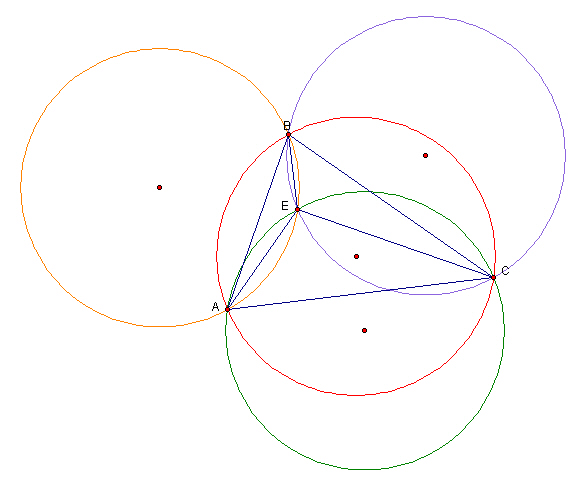
Do you notice anything special? What if we connect each circumcenter of the triangles AEC, AEB, and BEC to the two closest vertices of triangle ABC?
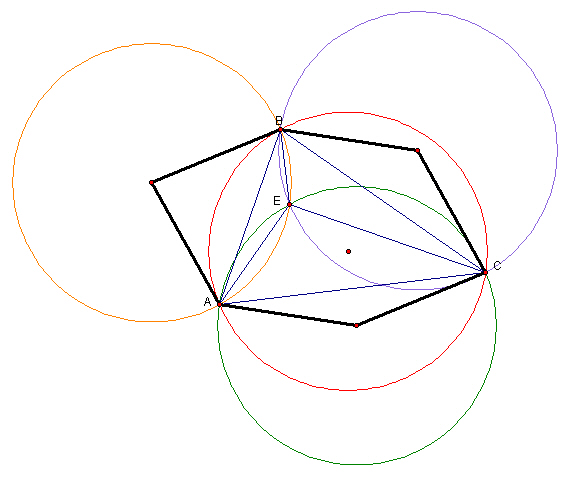
Do you notice anything now? Try reflecting the three triangles that you formed with the circumcenters and sides of triangle ABC across the sides that they share with triangle ABC.
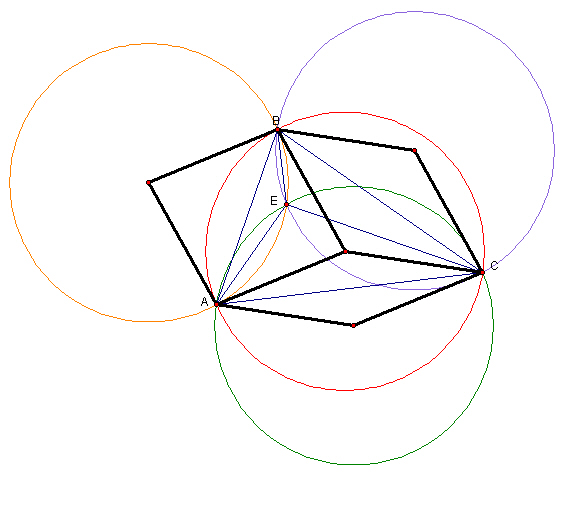
Do you have any conjectures now? Try manipulating this construction here.
I make the following conjectures:
1. The reflections of the circumcenters of the three triangles AEC, AEB, and BEC all correspond to the circumcenter of triangle ABC.
2. All four circumcircles are congruent. (That is the reflections of the circumcircles of the three triangles AEC, AEB, and BEC all correspond to the circumcircle of triangle ABC.
Can you prove these things with Euclidean geometry proofs? I tried using similar triangles, but I could not see a classical Euclidean proof, so I turned to coordinates.
Obviously proving 2 would prove 1. To prove 2, I need a claim.
Claim: Given a triangle, the reflection of its circumcircle across the line containing one of its sides will contain the orthocenter.
With the claim, we can handle the conjectures.
Proof of 1 and 2: A similar argument will work for each of the triangles AEC, AEB, and BEC. So let's use triangle AEC. We have shown that it has orthocenter B. By the claim, B is on the reflection of the circumcircle of triangle AEC about the line containing AC. Clearly A and C are also on this reflection. Thus, this reflection is a circle passing through A, B, and C. Hence the reflection of the circumcircle of triangle AEC across the line containing AC is precisely the circumcircle of triangle ABC.