Tom Cooper

---

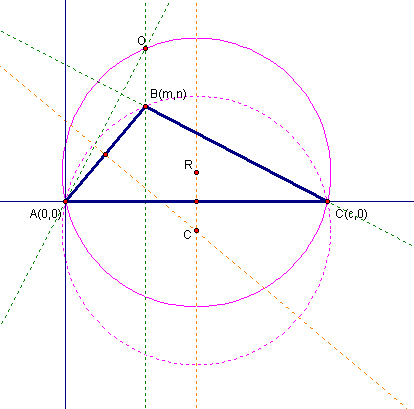
Claim: Given a triangle, the reflection of its circumcircle across the line containing one of its sides will contain the orthocenter.

Proof: Suppose that we have triangle ABC. Without loss of generality assume that we are going to reflect across the line containing AC. We will use a coordinate system by placing A at (0,0) and C on the x-axis. For convenience we can visualize this as follows:

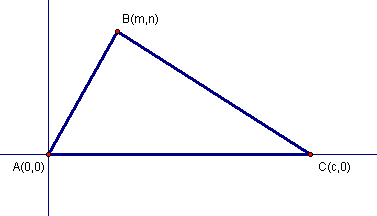
The proof will hold however, regardless of whether c, m, or n are positive or negative, i.e., the triangle need not be in quadrant I.

Let's begin by finding equations for the lines containing each side of the triangle.

AC is on the x-axis, so it is y = 0.

AB has slope (n-0)/(m-0) = n/m. Since it also passes through (0,0), it has equation y = (n/m)x.

BC has slope (n-0)/(m-c) = n/(m-c). This line with slope n/(m-c) and point (c,0) has equation y = [n/(m-c)](x-c).

Thus, we have the following lines

(1)        AC:      y = 0

(2)        AB:      y = (n/m)x

(3)        BC:      y = [n/(m-c)](x-c)

Now we can find two of the altitudes and get the coordinates of the orthocenter.

The simplest altitude to find is the one from vertex B to side AC. Since it is perpendicular to the x-axis and passes through B, it must satisfy x = m.

Now let's find the altitude from vertex A to the line containing BC.  Since this altitude is perpendicular to the line containing BC, it has slope -(m-c)/n. This line passing through (0,0) with slope -(m-c)/n has equation y = -[(m-c)/n]x. Since the orthocenter lies at the intersection of all three altitudes, it lies at the intersection of these two. Therefore the coordinates of the orthocenter of triangle ABC are (m, -[(m-c)/n]m) or equivalently (m, (-m² + cm)/n).

Hence, we have the orthocenter

(4)        O(m, (-m² + cm)/n)

Now let's see if we can find the circumcenter. Since the circumcenter of triangle ABC lies at the intersection of the perpendicular bisectors of the sides, we need to find at least two of these lines. It should be clear that the perpendicular bisector of AC is the vertical line x = c/2. Let's find an equation  for the perpendicular bisector of side AB. We can easily calculate that the midpoint of side AB is (m/2, n/2). In order for a line to be perpendicular to the side AB, it must have slope equal to (-m/n). This line with slope (-m/n) passing through (m/2, n/2) has equation y = n/2 + (-m/n)(x-m/2). The intersection of these two lines is the point (c/2, n/2+(-m/n)(c/2 - m/2)).

With a little distribution we get the following coordinates for the circumcenter

(5)        C(c/2, n/2 +(-cm + m²)/(2n))

Recall that we are trying to show that the orthocenter O lies on the reflection of the circumcircle about the line AC. Since AC is positioned on the x-axis, this reflection, call it R, has coordinates

(6)        R(c/2, -n/2 + (cm-m²)/(2n))

Observe that A and C must both lie on the reflection of the circumcircle of triangle ABC about the line AC since they are on the circumcircle and on the line. So we will be done with our proof if we can show that the distance from O to R is the same as the distance from O to A.

These distances are as follows:

(7)        O to R: d₁ =

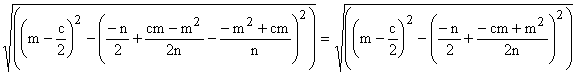
(8)        A to R: d₂ =

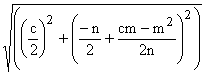
The reader can verify that these are indeed both equal and expand to 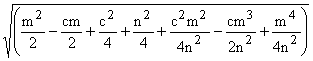.