
Final Assignment
by
Tom Cooper
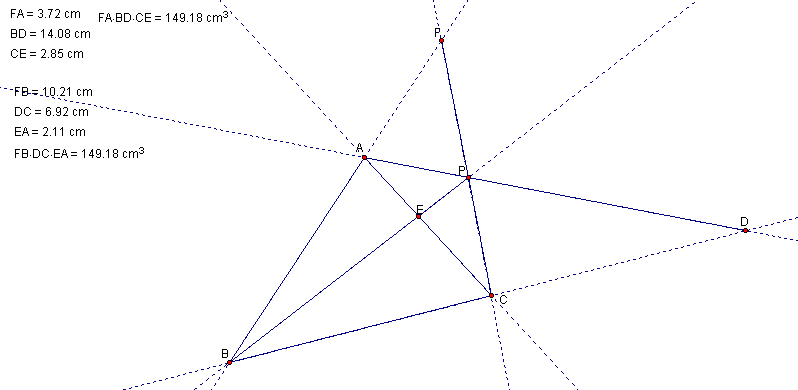
Consider a triangle ABC with an interior point P.
Construct the segments from each vertex through P to the opposite side.
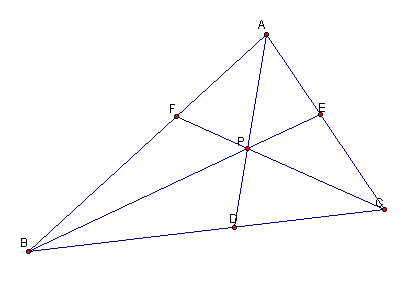

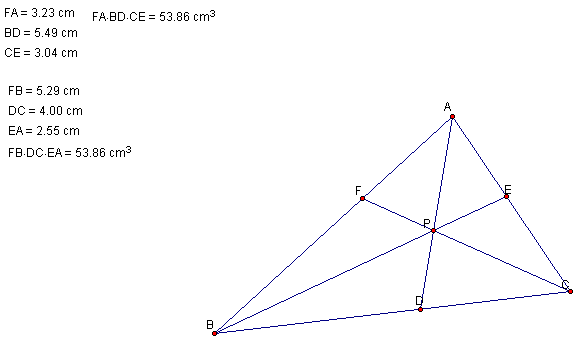
Exploring with this
GSP file, reveals that (AF)(BD)(CE) = (FB)(DC)(EA).
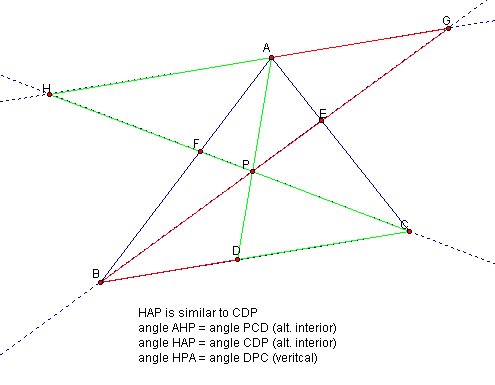

Let us try to prove this result. Following Dr.
Wilson's suggestion, we can draw a line parallel to side BC and extend CF and BE
to get some new triangles.
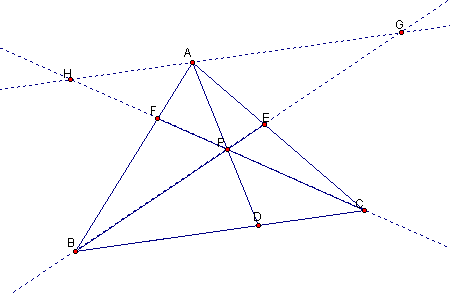

These parallel lines give lots of alternate
interior angles and several similar triangles.
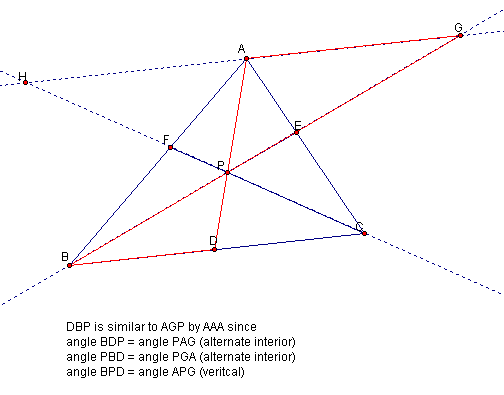

This gives the following equality of
ratios:
(*) (DP)/(AP) = (BP)/(GP) = (BD)/(AG)
(*) (DP)/(AP) = (BP)/(GP) = (BD)/(AG)

This gives us
(**) (AH)/(CD) = (AP)/(DP) = (HP)/(CP)
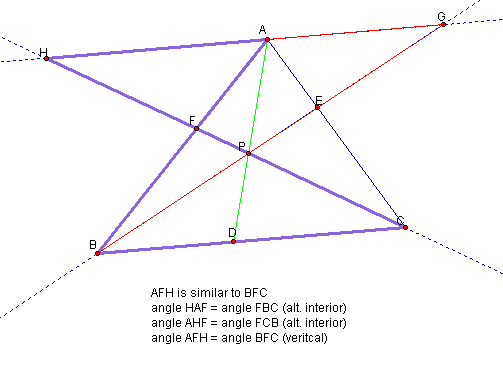
(**) (AH)/(CD) = (AP)/(DP) = (HP)/(CP)

Thus,
(***) (AF)/(BF) = (FH)/(CF) = (AH)/(BC)
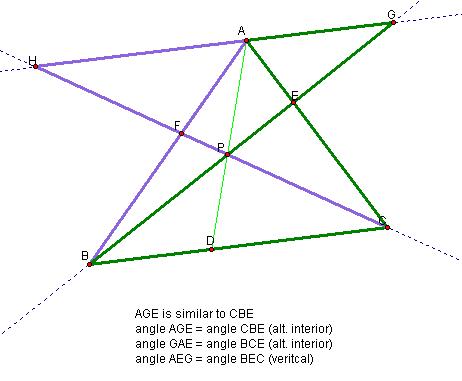
Hence,
(****) (CE)/(AE) = (CB)/(AG) = (EB)/(EG)
Now lets consider the ratio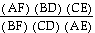 .
.
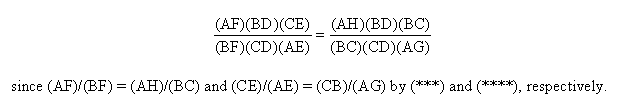
So,
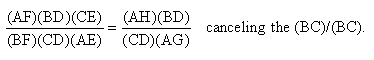
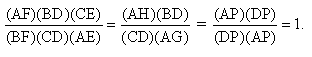
Therefore, we have shown (AF)(BD)(CE) = (FB)(DC)(EA).
If we extend the sides of ABC to lines, this result will hold even when P is outside the triangle.
(***) (AF)/(BF) = (FH)/(CF) = (AH)/(BC)

Hence,
(****) (CE)/(AE) = (CB)/(AG) = (EB)/(EG)
Now lets consider the ratio
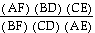 .
.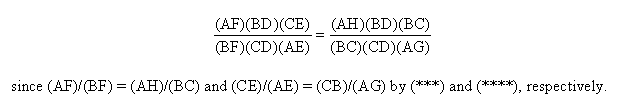
So,
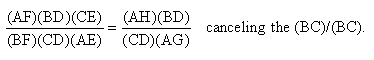
By (**) (AH)/(CD) = (AP)/(DP). Also, (BD)/(AG) = (DP)/(AP) by (*).
Hence,
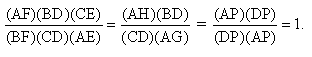
Therefore, we have shown (AF)(BD)(CE) = (FB)(DC)(EA).
If we extend the sides of ABC to lines, this result will hold even when P is outside the triangle.

Explore this here.
Now note that if P is the centoid then, triangle DEF is the medial triagnle.
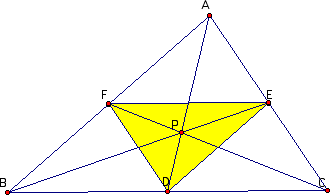
Now note that if P is the centoid then, triangle DEF is the medial triagnle.

It is fairly easy to show that the triangles AFE,
DFE, BFD, and DEC are congruent using the fact that DE || BA, DF || AC, FE ||
BC, and D, E, and F are midpoints.
Thus the area of triangle ABC is 4 times the area of triangle DEF.
Using my GSP file, you can see that the triangle DEF is smaller in area for every other interior point and thus the ratio is greater than 4 for all other interior points.
Thus the area of triangle ABC is 4 times the area of triangle DEF.
Using my GSP file, you can see that the triangle DEF is smaller in area for every other interior point and thus the ratio is greater than 4 for all other interior points.