__________________________________________________________________________________________________________________________________________
Part A
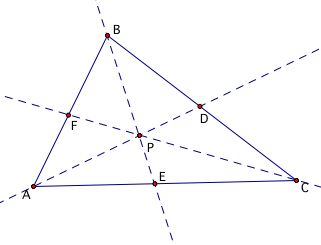
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F, respectively:

Now, let's consider the relationship between segments along the perimeter of the triangle ABC. For example, what is the relationship between (AF)(BD)(CE) and (FB)(DC)(EA)? Well, let's observe the segment measurements and the product of the respective segment measurements below:
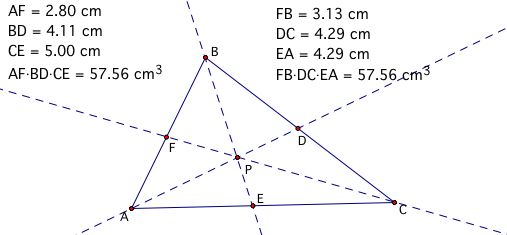
Notice how the product of (AF)(BD)(CE) = (FB)(DC)(EA). Regardless of the size of triangle ABC or the location of point P, this relationship holds. Click here to observe several variations (GSP 4.06 software required to view).
__________________________________________________________________________________________________________________________________________
Part B
Conjecture:
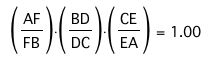
In order to prove this conjecture, it would be prudent to investigate similar triangles incident with triangle ABC. First, we will construct a parallel line to segment BC through point A. Then, compare the relationship between corresponding sides of the similar triangles for the four cases below:
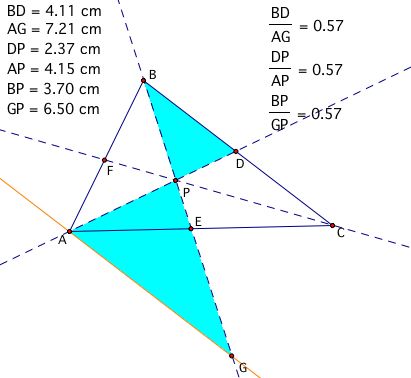
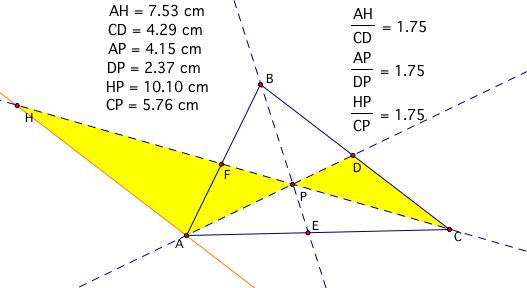
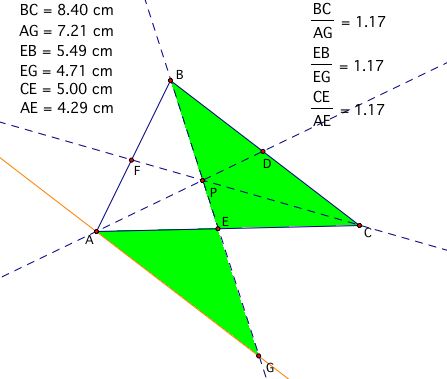
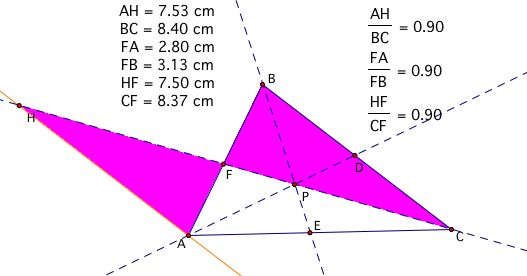
Notice the ratios of the corresponding sides of these similar triangles are equal for each of the four respective cases. Therefore, let's consider substituting these ratios into our conjecture formula to see if we come up with a proof of our conjecture.
Recall our conjecture:
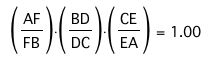
Now, find values to substitute. Recall that AF/FB = 0.90 and CE/AE = 1.17:
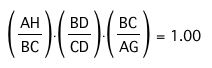
Notice BC cancels. Now, we have:
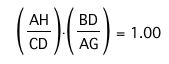
Now, substitute again. Recall that AH/CD = 1.75 and BD/AG = 0.57:
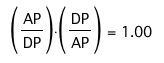
Notice AP and DP cancel with the result of 1 = 1. Therefore, we have proven our conjecture! To observe that this conjecture holds regardless of the location of point P, click here. (GSP 4.06 software is required)
__________________________________________________________________________________________________________________________________________
Part C
Show that when the point P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. Specifically, when is it equal to 4?
First, click here to observe that when point P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is in fact always greater than or equal to 4!!!
Then, observe the centroid point P of triangle ABC below:
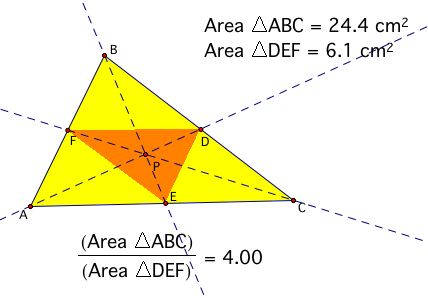
Notice that the area ratio equals 4!!! So, when point P is the centroid, the ratio of the areas of triangle ABC and triangle DEF is 4!!!
__________________________________________________________________________________________________________________________________________