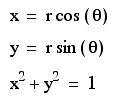
__________________________________________________________________________________________________________________________________________
What is a polar equation?
Simply stated: A polar equation is an equation which is represented in polar form. What does this statement mean? Well, suppose you have a point (2,3) and want to know the equivalent polar coordinates of this point. In polar form, this point looks like: (r, theta). This r is the distance from the origin to the point and the second coordinate, theta, is the angle created by the vector from the origin beginning at the positive x-axis to the point. The following are conversion rules:
______________________________________________________________________________________________________________________________________________________________
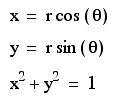
Let's begin our investigation with the following polar equation:
, where
a, b, k are integers.What happens when a=b=1, and k varies?
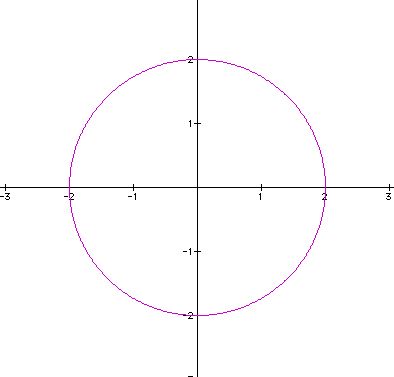
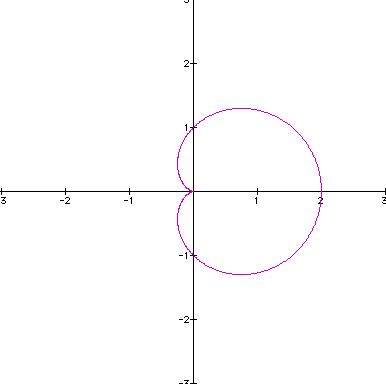
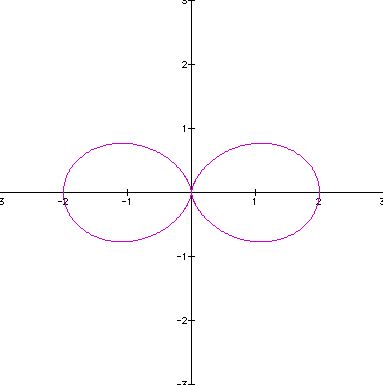
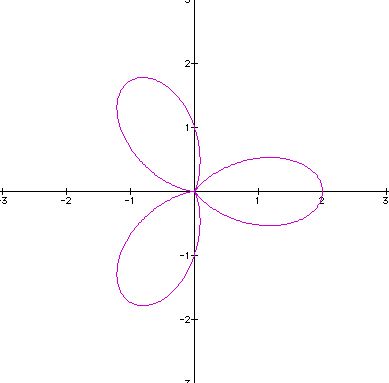
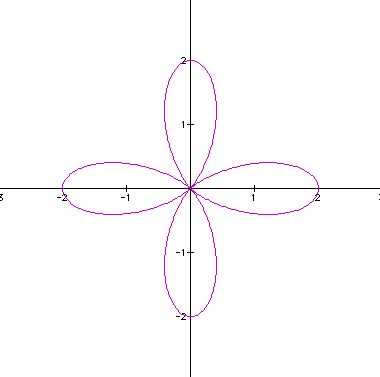
To view the animation where k = 1, 2, ..., 100, click here.
What pattern do you observe? Imagine this image is a flower, so we see that when k = 2, we have two petals, when k = 3, we have three petals, etc. This example is a textbook version of the "n-leaf rose".
______________________________________________________________________________________________________________________________________________________________
What happens when a > b and k = 1:
For the best visual, click here and here. In both cases a > b; however, a varies then b varies, respectively. One can imagine these images would alter when k varies, as well. Recall that the absolute value of k dictates how many "petals" are observed.
______________________________________________________________________________________________________________________________________________________________
What happens when a < b and k = 1:
Again, for the best visual, click here and here. In both cases a < b; however, a varies then b varies, respectively. Likewise, these images would change when k varies where the number of "petals" would match the absolute value of k.
______________________________________________________________________________________________________________________________________________________________
Now, what happens when we remove "a" from the equation?
, where b, k are
integers.Suppose k varies:
To observe where k = 1, 2, ..., 50, click here.
______________________________________________________________________________________________________________________________________________________________
Lastly, what happens when cosine is replaced with sine in our original polar equation?
, where
a, b, k are integers.Suppose a = b = 1, and k varies:
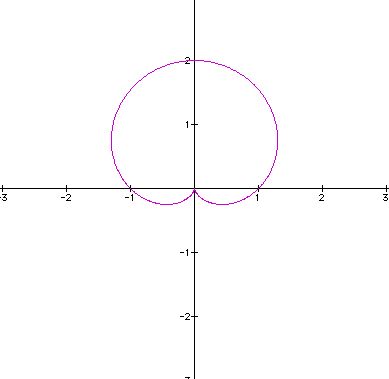
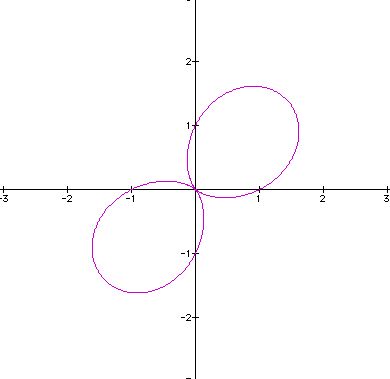
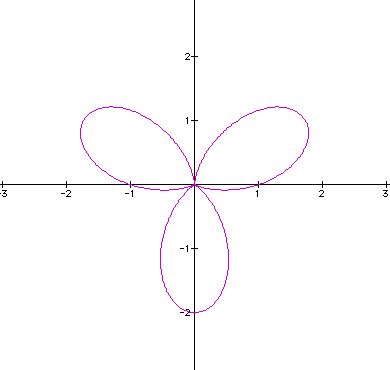
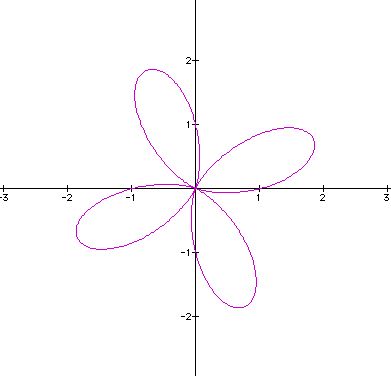
Like our previous example, click here to see how the image changes for k = 1, 2, ..., 100. When compared to our original cosine equation, these sine images have shifted by 90 degrees where k = 1, 45 degrees where k = 2, etc.
These investigations only begin to explore polar equations. However, this introduction provides a basis for further exploration in comparing Cartesian equations with polar equations.
__________________________________________________________________________________________________________________________________________