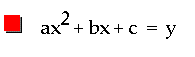
Let's begin this exploration with a review of the second degree polynomial:
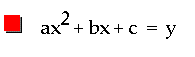
Now, observe the basic parabola, where a=1, b=0, c=0:
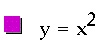
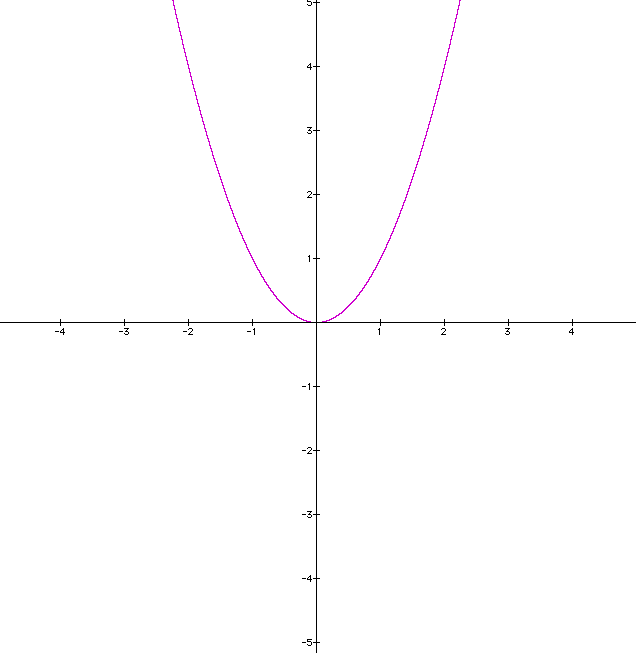
What happens when a=1, b=0, and c varies? To findout, take a look at this graph animation, where c oscillates between -5 and 5.
What happens when a=1, c=0, and b varies? To findout, take a look at this graph animation, where b oscillates between -5 and 5.
What happens when b=0, c=0, and a varies? To findout, take a look at this graph animation, where a oscillates between -5 and 5.
Our parabola can be manipulated with a change in a, b, and/or c.
How does it change?
When c changes value, we observe a shift along the y-axis. When b changes value, we observe a shift along the y-axis and the x-axis. When a changes value, we observe a symmetrical shift along the x-axis.