_______________________________________________________________________________________________________________________________
Using Geometer's Sketchpad 4.06, this assignment will investigate acute, right, and obtuse triangles, specifically the relationship between their defined CENTROID, ORTHOCENTER, CIRCUMCENTER, and INCENTER. First, let's review the definitions of acute, right , and obtuse triangles.
What is an acute triangle?
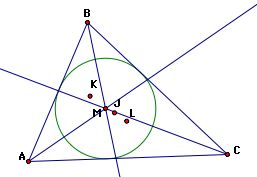
An acute triangle is a triangle where each interior angle is less than 90 degrees.
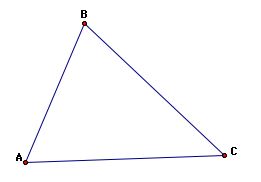
One can observe that all interior angles are less than 90 degrees here.
What is an obtuse triangle?
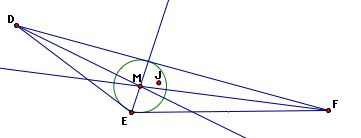
An obtuse triangle is a triangle where one interior angle is greater than 90 degrees.
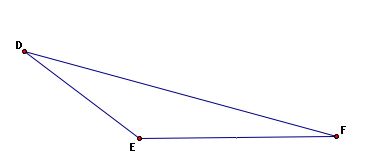
One can clearly see that the angle with vertex E is greater than 90 degrees.
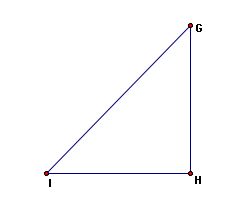
What is a right triangle?
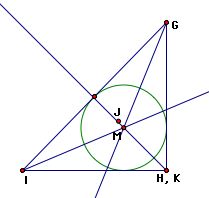
A right triangle is a triangle where one interior angle is equal to 90 degrees.
One can observe that the angle with vertex H is equal to 90 degrees.
_______________________________________________________________________________________________________________________________
Now, let's construct the centroid, orthocenter, circumcenter, and incenter for each of the above triangles. First, let's review the definitions of each center of a triangle and then witness each construction:
Centroid (J) - the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
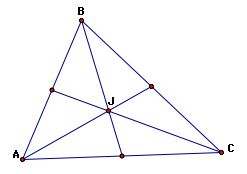
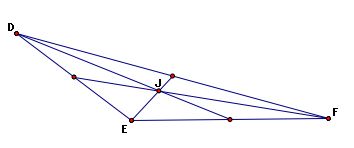
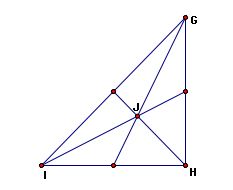
Orthocenter (K) - the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
Circumcircle (L) - the point in the plane equidistant from the three vertices of the triangle.
Q: How can we be sure this point is equidistance from each vertex?
A: Consider a circumscribed circle to the triangle. Does the radius vary as you travel around the circle? Of course not! So, the center of the circle is the same as the point equidistant from the three vertices of the triangle.
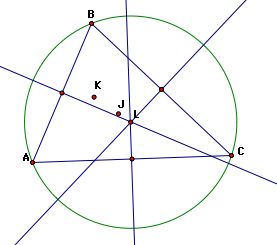
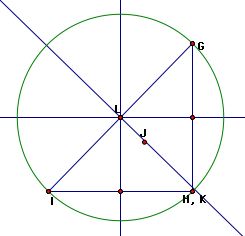
Incenter (M) - the point on the interior of the triangle that is equidistant from the three sides of the triangle.
Q: How can we construct this point?
A: Consider angle bisectors. Now, construct an inscribed circle to the triangle. Is the center of the circle the same as the intersection of our angle bisectors? YES!
_______________________________________________________________________________________________________________________________
Conclusions
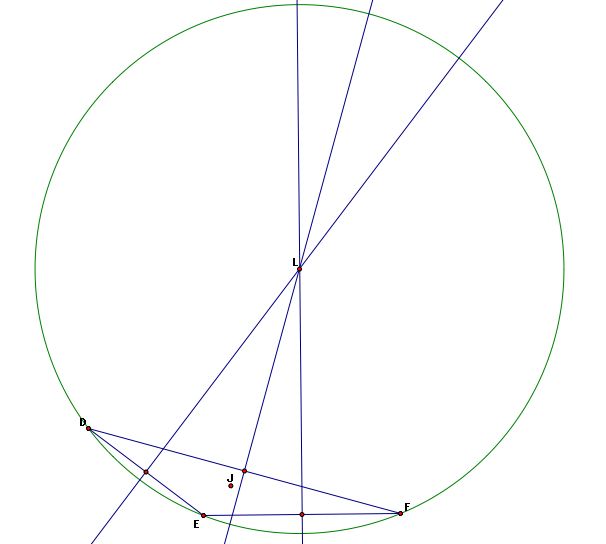
We observe that three of these points (J, K, L) have a linear relationship:
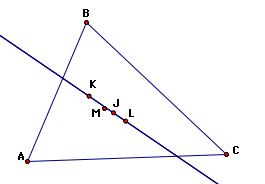
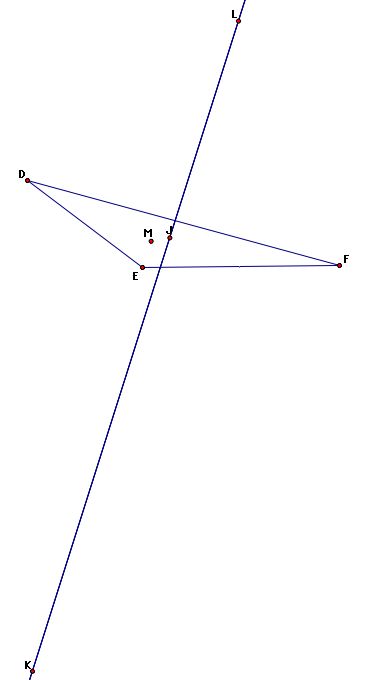
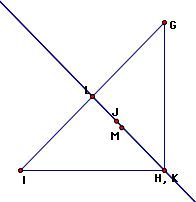
Finally, notice the centroid (J) and incenter (M) always lie in the interior of the triangles regardless of whether the triangle is acute, obtuse, or right.
Click here to see an animation of this fact. Also, notice as the triangle changes that the centroid (J), orthocenter (K), and circumcenter (L) remain linear.
Note: You must have Geometer's Sketchpad software to view this animation.