_______________________________________________________________________________________________________________________________
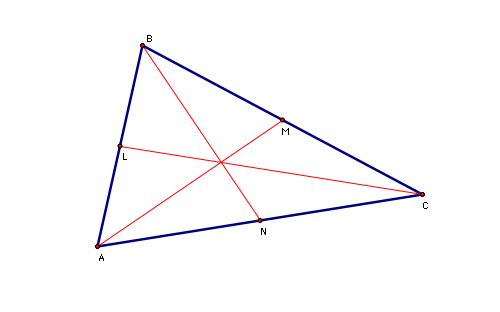
This assignment will explore triangle medians and their relationship to triangles. First, let's begin with a construction of a triangle and its medians:

Now, let's construct a triangle with the three sides having the same lengths of the three medians of Triangle ABC above. One way to explore this task is to consider Segment LC as one side of the new triangle. Then, construct parallel lines of Segment AM and Segment BN through points L and C, respectively. We will denote the intersection of the parallel lines as E.
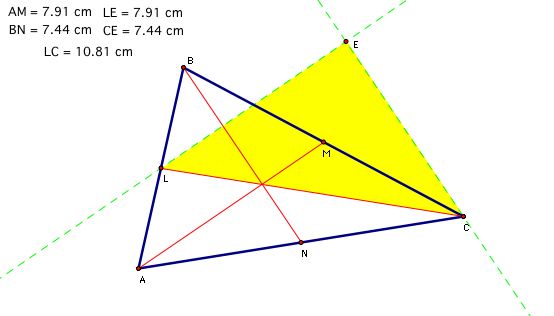
So, what is the relationship between Triangle ABC and Triangle LEC?
These triangles are not congruent or similar. They do not have the same area or perimeter. The ratio of perimeters is not constant. However, the ratio of area is constant.
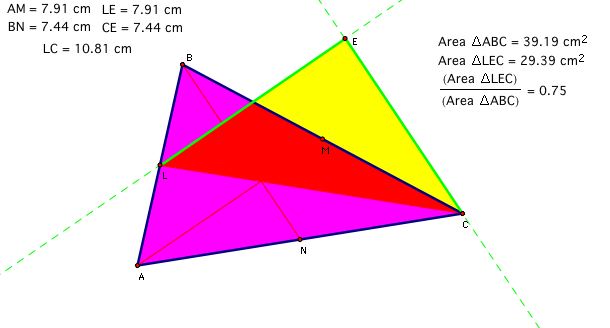
Also, the point of intersection, F, of Segment LE and Segment BC is the midpoint of Segment LE. Therefore, Segment CF is a median of Triangle LEC. Hence, there are more ratios of area which hold regardless of the size of Triangle ABC:
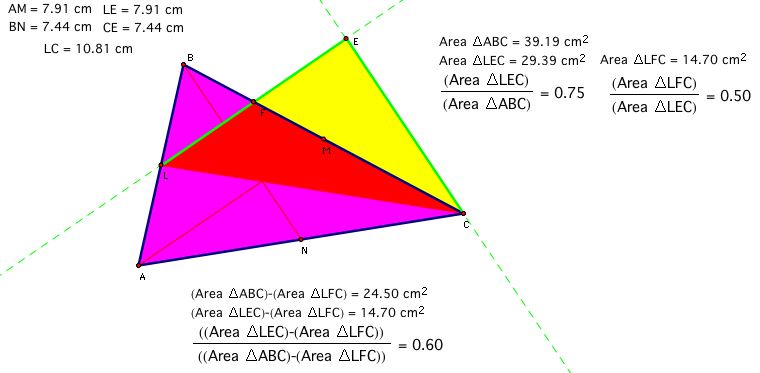
The area of Triangle LEC is exactly 0.75 of the area of Triangle ABC. The Triangle LFC is exactly half the area of Triangle LEC. And, the ratio of the yellow area to the pink area (above) is exactly 0.60. These ratios hold regardless of the size of Triangle ABC. To witness this relationship for yourself, please click here (you will need GSP 4.06 software to view).