___________________________________________________________________________________________________________________________________________
This assignment will explore the relationship of altitudes and orthocenters of a given acute triangle.
First, let's construct an acute triangle ABC:

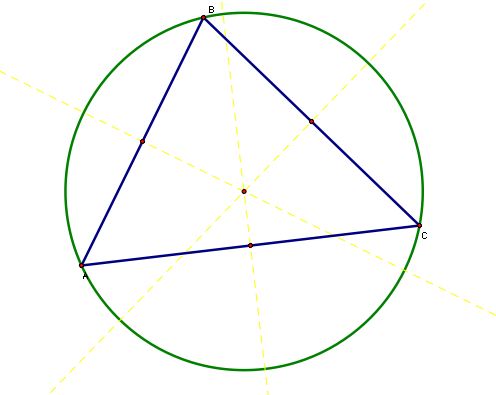
Next, let's construct its circumcircle:
Now, consider the three altitudes of triangle ABC -- AD, BE, and CF:
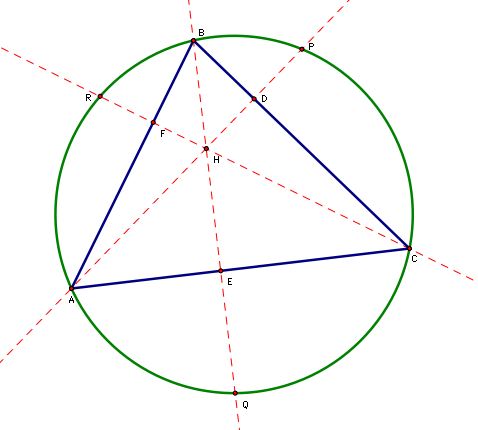
Recall that the intersection, H, of the altitudes of a given triangle is called the orthocenter of the triangle. This direct relationship between altitudes and the orthocenter is obvious. However, the relationship between the respective altitudes to the extended segment that intersects the circumcircle is not obvious.
Let's consider the sum of the ratios of these extended segments to their respective altitude segments. In other words, what is the sum of:
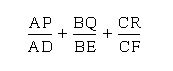
Well, when the orthocenter, H, is in the interior of the triangle ABC or on the perimeter (i.e. at one of the vertices)...the sum is always 4!!! However, if you manipulate the size of triangle ABC and the orthocenter moves to the exterior of triangle ABC, then there is no defined sum!!! Why?
Well, consider the altitudes of an obtuse triangle. The above summation does not represent a consistent relationship between the respective altitudes of an obtuse triangle.
Note: To explore this manipulation for yourself, please click here. (you will need GSP 4.06 software to view)
Now, consider the location of the orthocenter and the changes in values of the altitudes as you manipulate the size (i.e. acute, obtuse) of triangle ABC. Notice when triangle ABC is acute, the sum of 4 holds. However, when triangle ABC is obtuse (i.e. when the orthocenter is on the exterior of the triangle), the sum of 4 does not hold.
Moreover, this sum of 4 holds when the orthocenter is in the interior or on the circumference of the circumcircle, too!
__________________________________________________________________________________________________________________________________________