Assignment 10: Explorations of Parametric Curves
by Kristina Dunbar, UGA
Parametric curves in the plane are a pair of functions of the form:
x = f(t)
y = g(t)
where the two continuous functions define ordered pairs (x,y). These two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t.
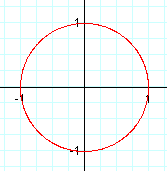
Let's graph:
x = cos (t)
y = sin (t)
Because we are dealing with cosine and sine functions, we know that the normal period is 2π, so let's let t range from 0 to 2π.

What if t didn't range from 0 to 2π? What if it ranged from the following?
0 ≤ t ≤ 1 0 ≤ t ≤ π π/2 ≤ t ≤ 3π/2
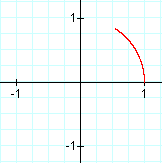
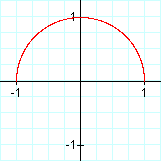
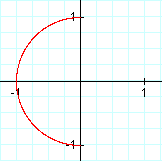
We see that t is the angle θ that the curve sweeps out, where θ = 0 has the coordinates (1,0), θ = π/2 has the coordinates (0,1), and so on.
This should remind you of cut-outs of the unit circle.
Now let's investigate the equations
x = cos (at)
y = sin (bt)
where 0 ≤ t ≤ 2π.
====+=+=+=+=+=+=+=+=+=+====
1. Let a = b, and a not 1.
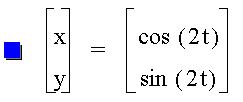
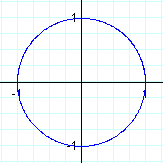
It looks exactly the same as the earlier graph, where a = b = 1.
====+=+=+=+=+=+=+=+=+=+====
2. Let a > b.
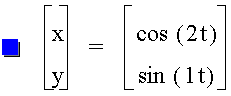
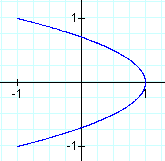
This looks like a parabola!
+++==========+++
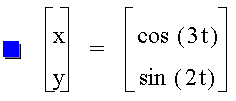

Interesting, it looks like two boomerangs.
+++==========+++
Let's try it again:
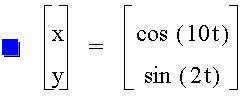
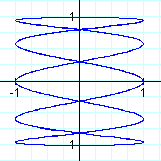
+++==========+++
Once more:
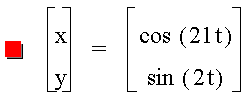
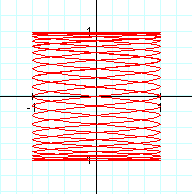
====+=+=+=+=+=+=+=+=+=+====
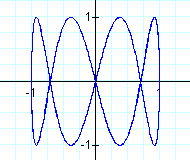
3. Let a < b
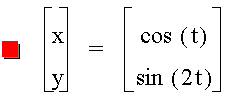
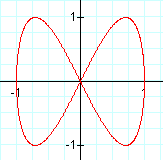
+++==========+++
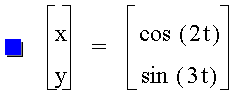

+++==========+++
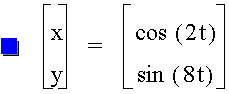
+++==========+++
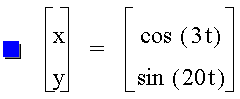
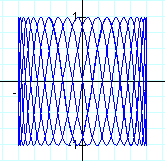
These types of curves are actually called Lissajous curves, and there is a great website with an interactive lab you can explore here.
Now let's investigate the equations
x = a cos (t)
y = b sin (t)
where 0 ≤ t ≤ 2π.
====+=+=+=+=+=+=+=+=+=+====
1. Let a = b, and a not 1.
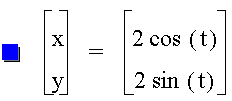
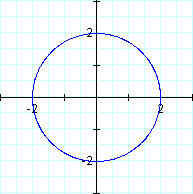
It retains the same shape as the original equations, but the radius of the circle increases to the amount a.
+++==========+++
Let's put a few of these graphs together and see how it looks:
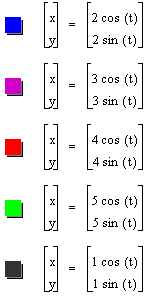

====+=+=+=+=+=+=+=+=+=+====
2. Let a > b.
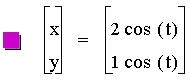
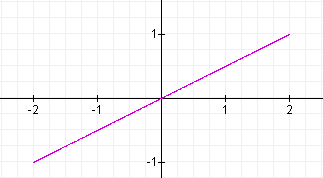
We get a straight line with a slope of .5, or b/a.
+++==========+++
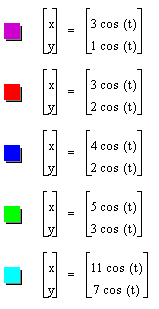
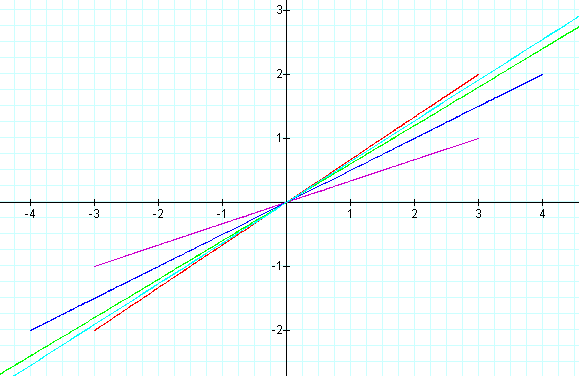
The length of these straight lines is actually 2√(a2 + b2).
====+=+=+=+=+=+=+=+=+=+====
3. Let a < b.
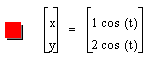
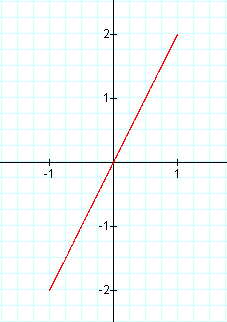
This looks like it will be the exact same thing as when a > b; the slope of the line is still b/a and the length of the line is still 2√(a2 + b2).
Return to my Home Page.
Some good links for Lissajous Curves:
Lissajous Curves - from Math World