Assignment 11: Polar Equations

by Kristina Dunbar, UGA

In this assignment, we will be exploring polar equations of the form

r = a + b cos (kθ)

for different values of a, b, and k. 

We will start by letting a and b be equal and varying k. 

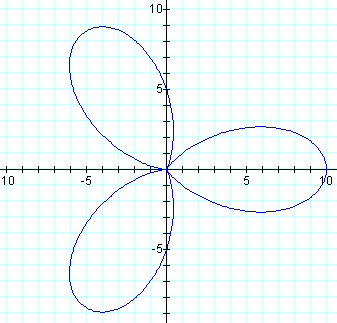
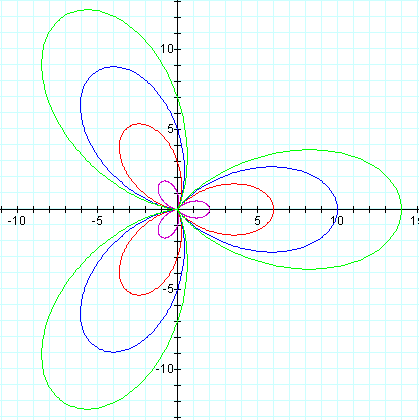
When a = b, we have a "k-leaf rose", often referred to in textbooks. 

As long as the values of a and b are equal, the graph will not change shape, only size.

Now let's vary k:

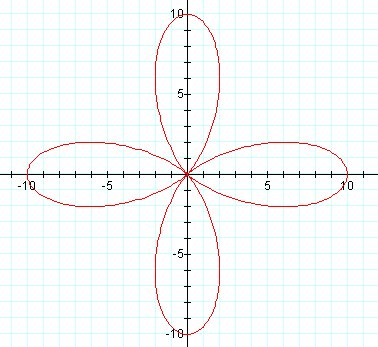
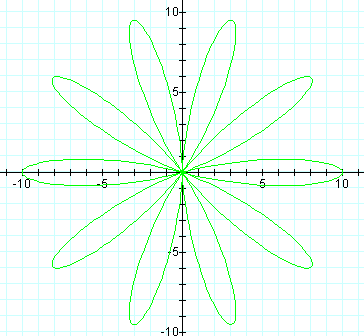
It is clear that varying k will vary the number of leaves or petals on your flower. 

What if a ≠ b?

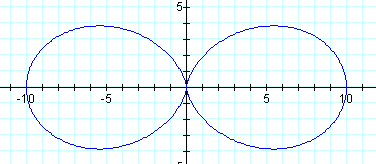
Let's first start with a = 0, so we are left with the equation

r = b cos (kθ)

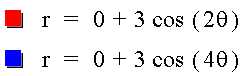
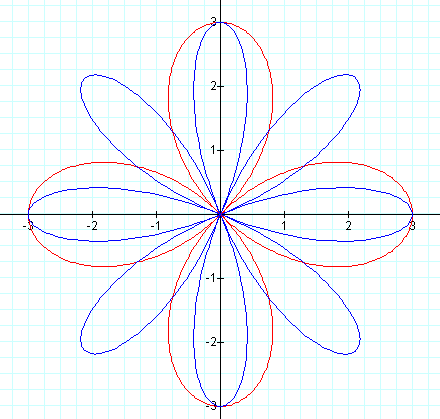
For even numbered k with a = 0, the number of leaves of the flower are actually 2k. 

This is not the case with odd-number k, as soon below:

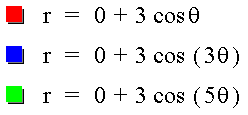
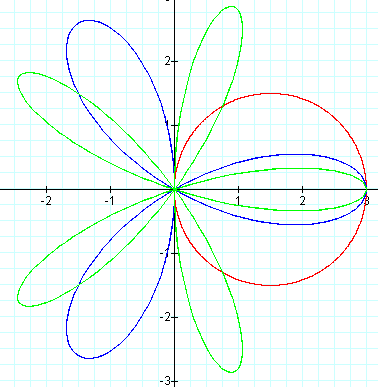
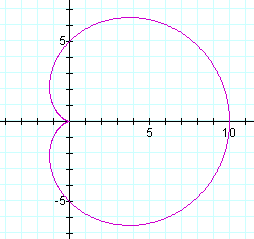
In the case of a = 0 and an odd-numbered k, we see that the first petal is centered around the x-axis (θ = 0) and has an amplitude of b.  Also for an odd-numbered k, we see that there are k-leaves to the flower. 

Notice that when k = 1, we have a perfect circle.

Now, let a≠b, with a and b both non-zero.

First, we'll try a case where a < b.

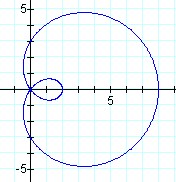
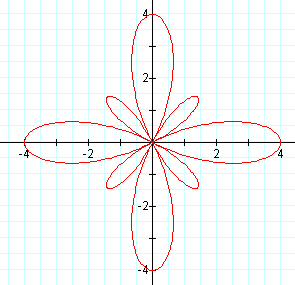
There are 8 loops (or 2k) loops.  There are four major loops & four minor loops.  The major loops have an amplitude of a + b, and the minor loops have an amplitude of b - a. 

Let's look at one more case to make sure we're on the right track.

It looks like we're on the right track!  The larger loops have an amplitude of 5, while the smaller loops have an amplitude of 1.

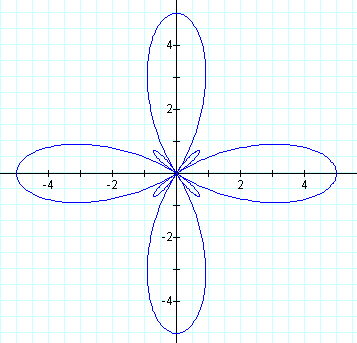
Now, let's look at a case where a > b.

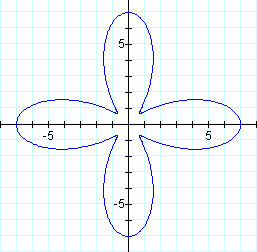
The loops no longer intersect at the origin and look more like petals now.  The petals still have an amplitude of a + b.  They intersect at a distance a - b away from the origin.

Let's look at a few more to be sure:

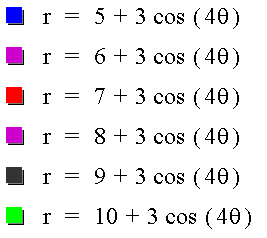
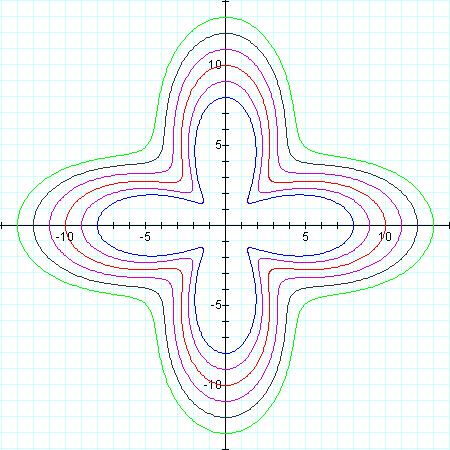
Looks like we have the right idea!

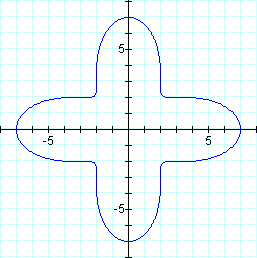
Another thing to note about this type of graph is that when k is odd, the secondary (smaller) petals appear inside the larger ones, instead of between them.

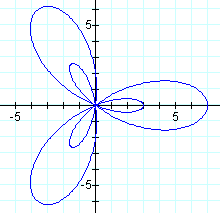
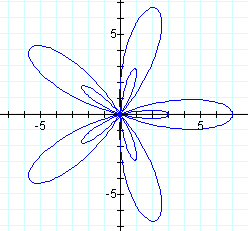
Let's look at one more investigation of this equation. 

What if we changed cos θ to sin θ?

Here are a few graphs of interest:

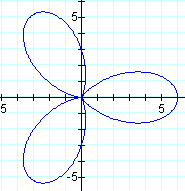
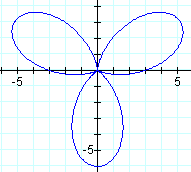
Changing cosine to sine made the first petal center around the -π/2 axis instead of the 0 axis.

Let's look at one or two more:

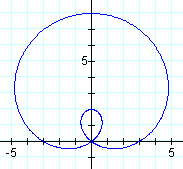
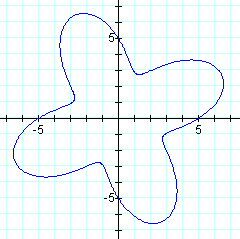
It looks like changing the cosine function to the sine function in the above graphs retains the shape of the original figure, but changes the orientation.

Return to my Home Page.