Fibonacci Sequence in Excel

by Kristina Dunbar, UGA

In this assignment, we will be investigating the Fibonacci Sequence using Excel.  As we all know, the Fibonacci sequence is of the form: 

f(n) = f(n-1) + f(n-2)

To generate the Fibonacci sequence, f(0) and f(1) both equal 1.  You can use the equation above to obtain the rest of the Fibonacci numbers.

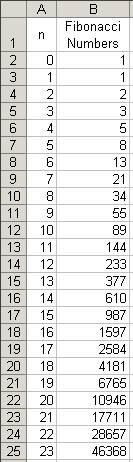
We see that the Fibonacci Sequence gets very high very fast. 

What about the ratio of adjacent terms in the Fibonacci sequence? 

We can use Excel to find this, as well.  Just add another column, where the entries in that column equal the entry to the left divided by the entry to the left and up one. 

Example:  C5 = B5/B4.

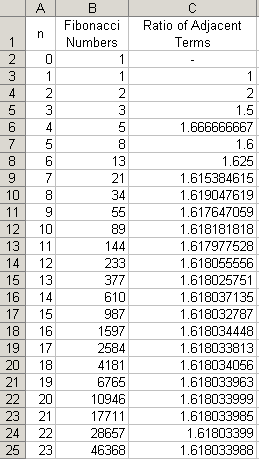
We see that the limit of the ratio of successive terms is 1.618, also known as the golden mean or golden ratio, Φ.

What about the ratios of every second term?

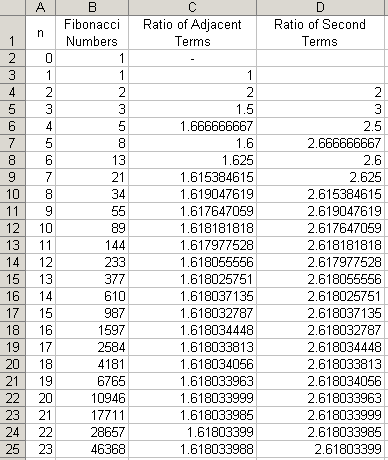
The limit of this ratio goes to 2.618.  But, what's special about 2.618?  It's the golden ratio squared!

1.618² = 2.618

What about the ratios of the third terms?

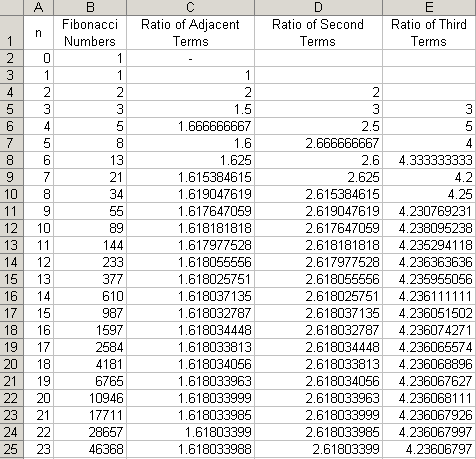
Can you guess what 4.236 is?

That's right, it's the golden ratio cubed.

1.618³ = 4.236

The golden ratio is often represented by the Greek letter phi, or Φ.

The ratios of the fourth, fifth, sixth terms, etc. will be the golden ratio that that power.

Ratio of adjacent terms    =    Φ

Ratio of every 2^nd term    =    Φ²

Ratio of every 3^rd term    =    Φ³

Ratio of every 4^th term    =    Φ⁴

Ratio of every 5^th term    =    Φ⁵

^{You can click here for the Excel spreadsheet used to generate the above data.}