Assignment 6:  Explorations with Geometer's Sketchpad

Parabola Construction

by Kristina Dunbar, UGA

A parabola is the set of points equidistant from a line, called the directrix, and a fixed point, called the focus.  A traditional parabola looks like the figure below:

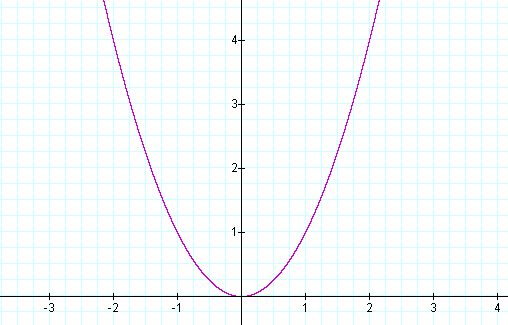
But, how do we construct it?

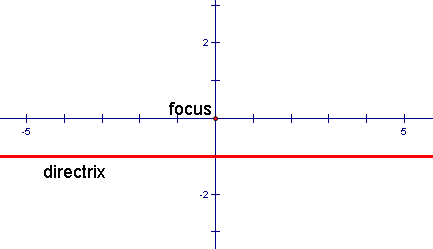
1.  We'll start by identifying a directrix and a focus. 

• The directrix can be any line.  In the below case, we chose y = -1 as the directrix. 

• Likewise, the focus can be any point.  In the below case, we chose the origin to be the focus.

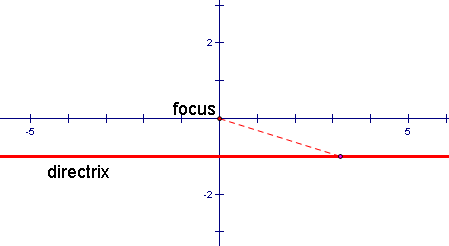
2.  Next, we will place a movable point on the directrix and construct a line from the movable point to the focus.

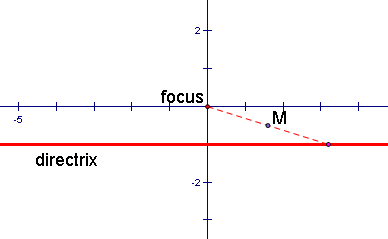
3.  Now we need to construct the midpoint of the line segment between the focus and the movable point on the directrix.

4.  We will now create two perpendicular lines:

• One will be at the movable point on the directrix and will be perpendicular to the directrix.

• The second will be at the midpoint of the line between the directrix and focus at the point M and perpendicular to the dotted line segment.

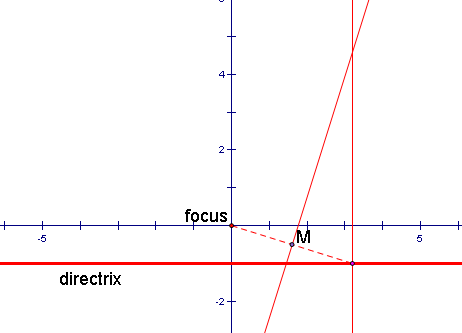
5.  We will now mark the intersection of these two parallel lines.  This point will be on the locus of the parabola.

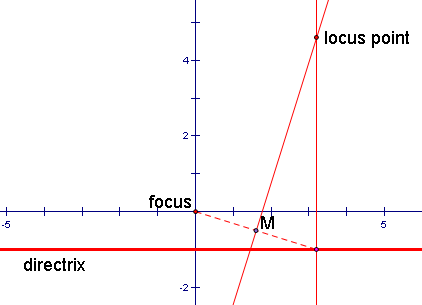
6.  Finally, if we animate the point on the directrix and trace the locus point, we will get the parabola pictured below in blue.

We have now created a parabola.

Return to my Home Page.

Return to TOP.

Now that we know how to construct a parabola, there are a few other neat things we can do. 

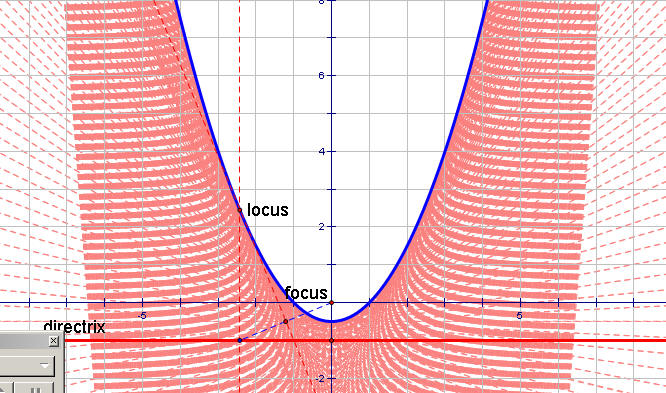
Notice that the line from the midpoint M to the locus point is always tangent to the parabola, even though it moves around.  If we trace this line, here is what it will look like:

What if we trace the midpoint M?  What do you think it will do?

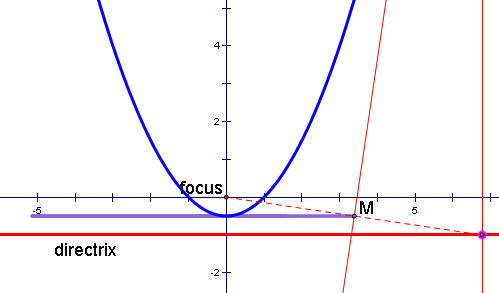
Even though the midpoint M of the segment between the movable point on the directrix and the focus moves, it stays in a straight line. 

This straight line is:

• Halfway between the focus and directrix, so in this case M traces the line y = -1/2

• Tangent to the very bottom of the locus.

Click here for a GSP construction of the locus.

Click here for further explorations of the parabola.

Return to my Home Page.

Return to TOP.