by Kristina Dunbar, UGA
![]()
In this assignment, we will investigate a circle tangent to two given circles. We will use GSP to make a construction of this problem. The final result will look like the figure below.
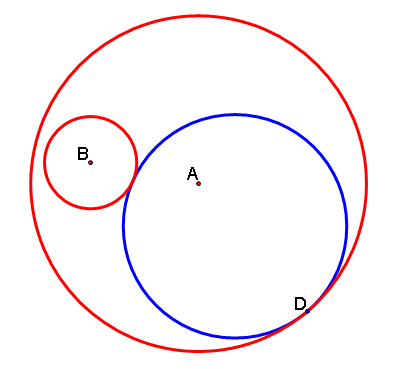
![]()
Section 1: How do we make the construction?
1. First, start with what we are given: two circles, one inside the other with origins A and B.
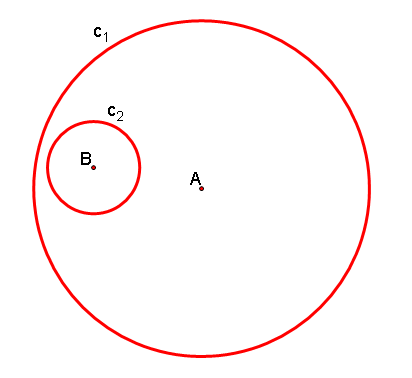
2. Next, we will place movable points on each circle by using the "point on object" command in GSP.
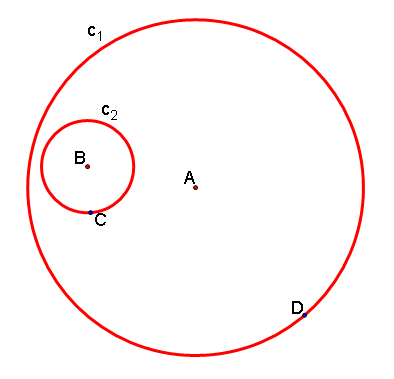
3. Now, we will construct a line segment from B to C which will be the length of the radius of circle c2. We will also create a line going through points A and D.
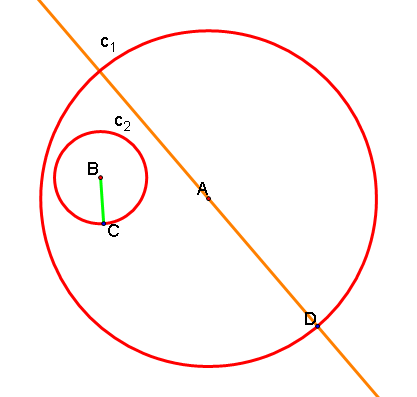
4. Next, we will construct a circle with center at movable point D and radius BC.

5. Finally, we will construct the outer intersection of the circle c3 with the orange line passing through AD.
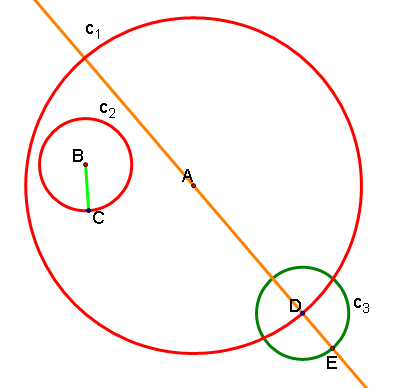
6. Now, draw line segment BE and construct its midpoint M.
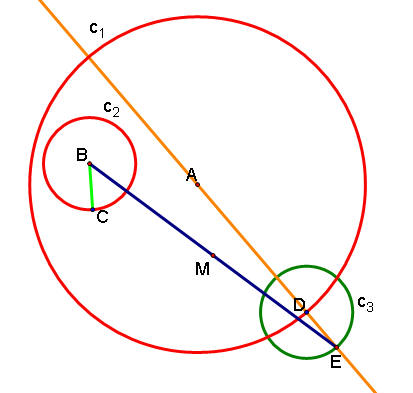
7. Draw a line perpendicular to line segment BE through M. Mark its intersection (G) with the orange line AD.
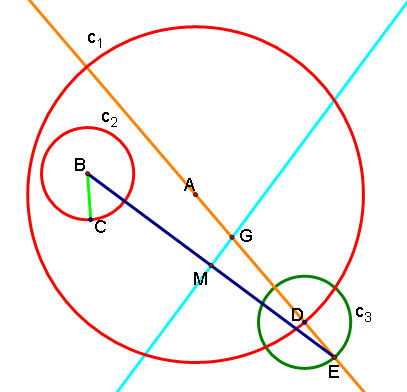
8. Now you can construct circle c4 with center at G and radius GD. This new circle is the circle that's tangent to the two given circles!

If we hide all of the construction aids, we will see that this is the picture at the top.

Click here for a GSP Script creating a circle tangent to two given circles. The first page of the file contains the construction without all of the construction lines visible; page two shows the construction lines.
![]()
Return to my Home Page.
Return to TOP.
Return to Section 1.
Skip to Section 2 or Section 3.
![]()
We know by construction that the points C and D are movable. How does that affect the tangent circles?
Moving point C around circle c2 will not change anything because it was just used to construct a radius.
But what about point D?
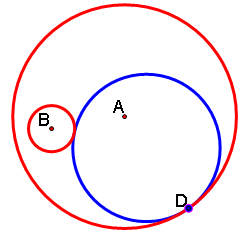
It turns out that if we animate the point D, circle c4 remains tangent to both circles c1 and c2, but it changes size as D moves around circle c1.
You can click here for a GSP animation of this (make sure point D is highlighted), or look at some examples below.
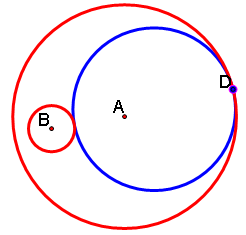
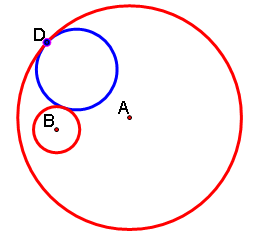
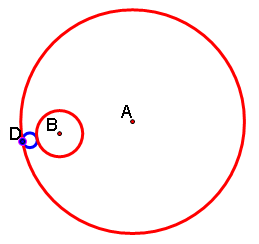
![]()
Return to my Home Page.
Return to TOP.
Return to Section 1 or Section 2.
Skip to Section 3.
![]()
What does the center of our new circle c4 look like as D is moving around?
We see that the center of our new circle c4 (point G) moves in an ellipse with foci A and B.
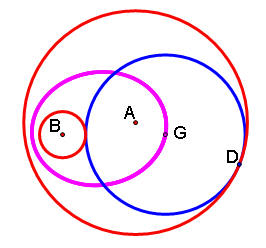
In fact, we see that if we construct a line segment AG, it will sweep out the entire ellipse.
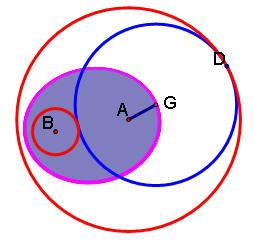
Click here to see this GSP construction. Just make sure point D is highlighted and click on the animate button to see the ellipse traced out.
![]()
Return to my Home Page.
Return to TOP.
Return to Section 1 or Section 2 or Section 3.
![]()