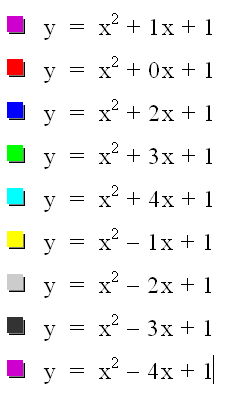
Assignment 3:
Further exploration of
In Assignment 2 we examined the parabolas of the equation
In the assignment we varied the values for a, b, and c and noted how the parabolas changed with the different values. In one case we held b and c constant while varying a. In another we held a and c constant while varying b. In the last case, we help a and b constant while varying c.
Chick here to review this investigation.
In Assignment 3, we will be concentrating on the parabolas formed from the equation
when we vary the value for b.
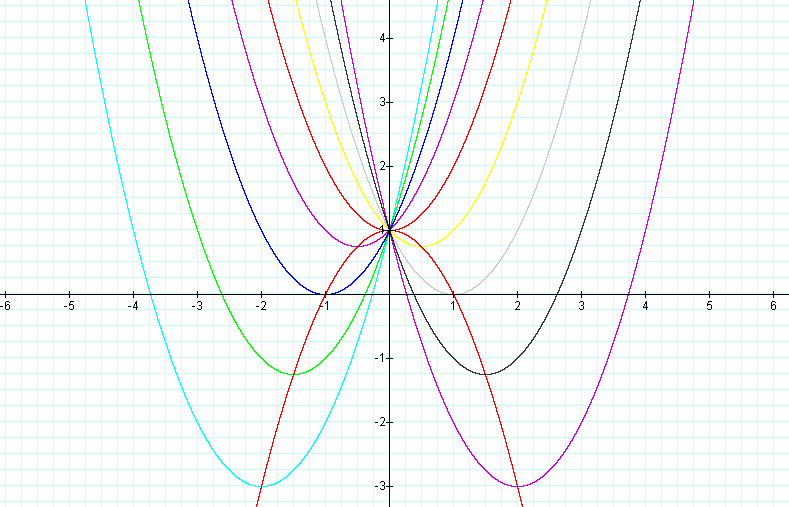
The following is a graph of y = ax2 + bx + c with varying values for b.
There are a few important things to notice while investigating the above graph of the parabolas:
Notice that each of the parabolas passes through the point (0,1) on the y-axis.
When b is less than -2, the parabola will intersect the x-axis in two points with positive x-values (i.e. the original equation will have two real roots, both positive).
When b is equal to -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency.
When b is between -2 and 2, the parabola does not intersect the x-axis (the original equation has no real roots).
When b is equal to 2, the parabola is tangent to the x-axis (one real negative root).
When b is greater that 2, the parabola intersects the x-axis twice to show two negative real roots for each b.
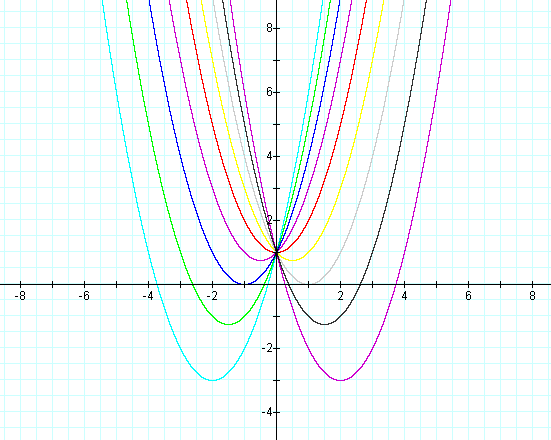
Now, lets look at the vertices
of each of the parabolas that we have graphed above and notice that the locus of
the vertices of our parabolas above create a parabola with the vertex at (0,1)
and an equation of
![]() .
.