Assignment 7:
Tangent Circle
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
Steps to Follow in Constructing Tangent Circles
Step 1: Construct the given two circles. Make on circle larger than the other, with the smaller circle inside the larger circle.

Step 2: Construct a point on the larger circle by selecting the larger circle and using the Construct tab on the tool bar. Then select 'Point on Circle'.
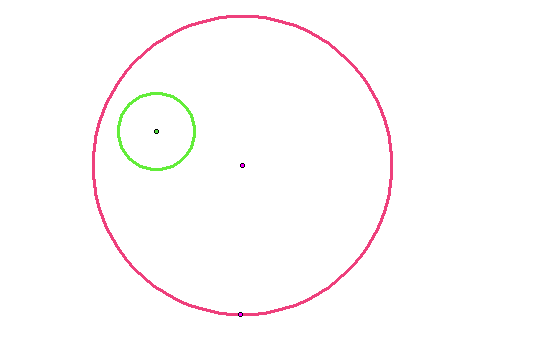
Step 3: Construct a point on the small circle using the same steps as in Step 2. Then, construct a segment from the center point of the small circle to the point on the small circle that was just constructed.
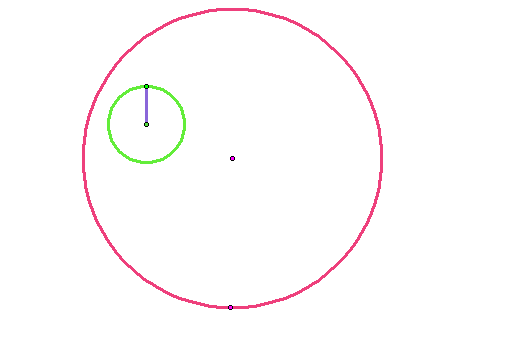
Step 4: Construct a line going through the center of the large circle and the point that we constructed on the large circle in Step 2.
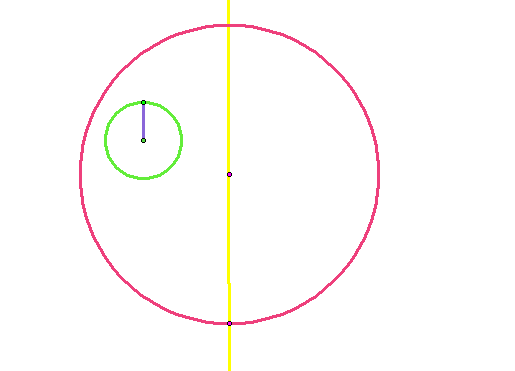
Step 5: Now we need to construct another circle using the point on the larger circle and the radius of the smaller circle. To do this, first select the point on the larger circle and then select the segment that marks the radius of the smaller circle. Next, select Construct from the tool bar and then select 'Circle by Center + Radius' from the options.
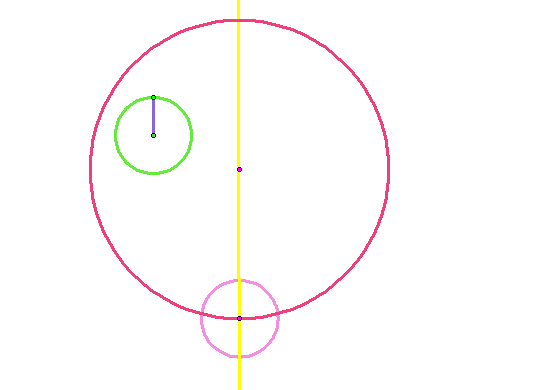
Step 6: Construct the intersection point of the circle constructed in Step 5 and the line constructed in Step 4. There are two point that intersect the line ... construct the one that is outside of the larger circle.
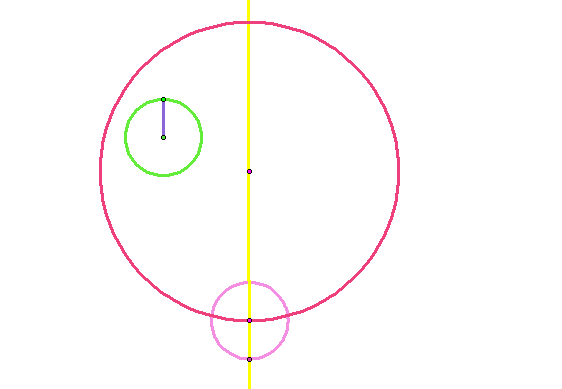
Step 7: Construct a segment (blue) from the intersection constructed on Step 6 to the center of the smaller circle (green).
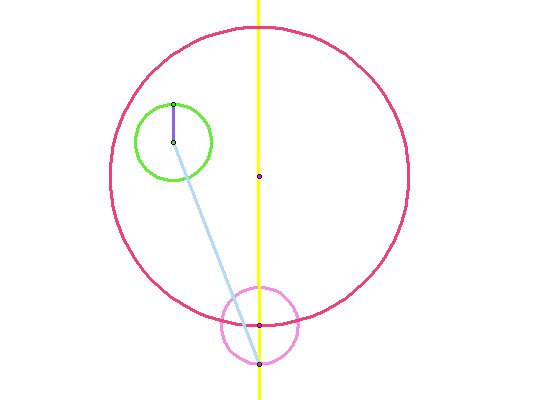
Step 8: Construct the midpoint of the segment (blue) constructed in Step 7.
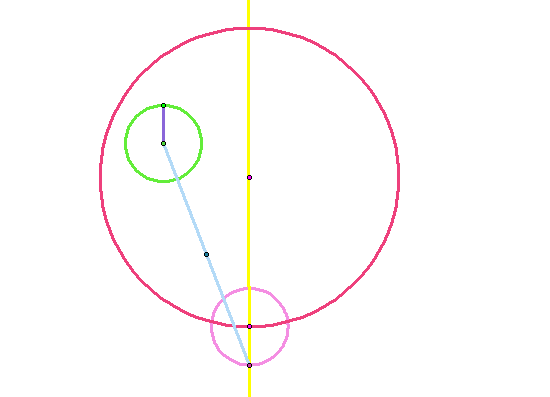
Step 8: Construct a line perpendicular to the segment (blue) constructed in Step 7 and the midpoint constructed in Step 8.
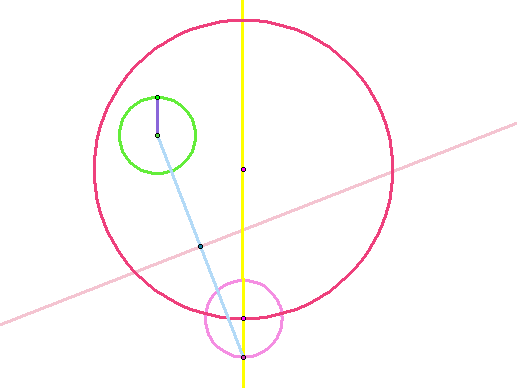
Step 9: Construct the point of intersection between the line constructed in Step 4 and the perpendicular line constructed in Step 8.
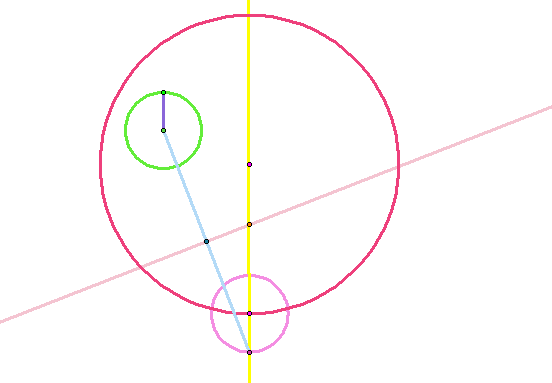
Step 10: Construct a circle using the intersection point constructed in Step 9 as the center and passing through the center point of the circle constructed in Step 5. This circle is constructed using the option 'Circle by Center + Point'. This is our circle that is tangent to the given two circles!
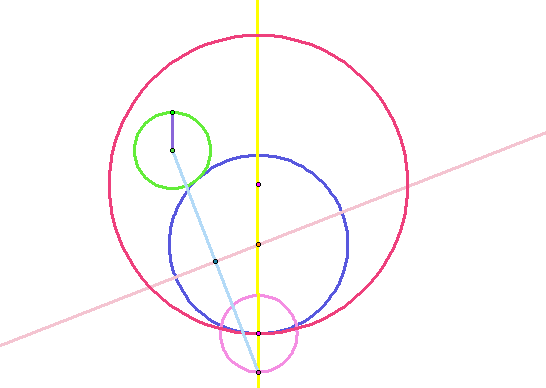
Will This Circle Always be Tangent to Both of the Given Circles?
Click here to see the animation of the point on the larger circle. As you can see, as the point on the larger circle moves around the circle, the blue circle that we constructed remains tangent to the two given circle. Also notice that the clue circle changes in size as the center point follows the perimeter of the larger circle so that it remains tangent to both circle.
Wouldn't it be nice to have a Script Tool to Construct These Tangent Circles to Use for Future Investigations of Tangent Circles?
Click here for the script tool of the tangent circles that we have constructed in Assignment 7.