Assignment 8:
Altitudes and Orthocenters
What are Altitudes and Orthocenters?
Given any triangle, an altitude of the triangle is the line perpendicular to one of the vertices and the corresponding opposite side of the triangle. Three altitudes may be constructed on a given triangle.
The orthocenter of the triangle is the intersection point of the three altitudes.
Lets Construct a Triangle and Investigate the Orthocenter
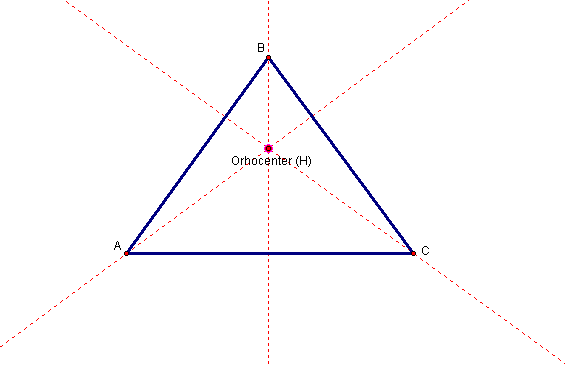
Below is the triangle ABC with the altitudes and the orthocenter constructed. Click here for instructions on how to construct the orthocenter of a triangle using GSP.

Look! The Orthocenter of the Triangle ABC Created Three More Triangles
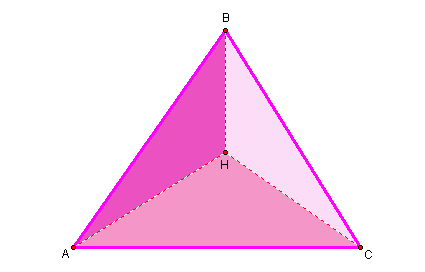
Notice, when we created the orthocenter of triangle ABC, we divided the triangle into three more triangles (HBC, HAB, and HAC). Below are the three triangles shaded in the original triangle ABC to make them easier to see.
Let's Find the Orthocenter of the Three New Triangles
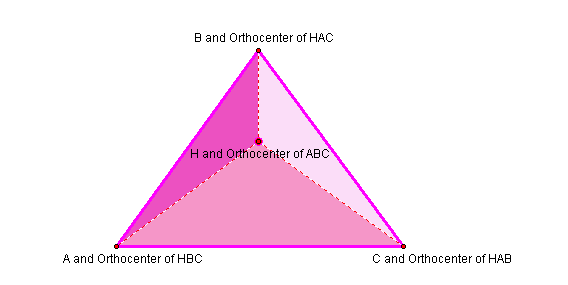
Notice that the orthocenters of the three triangles are the vertices of the triangle ABC.
Click here to investigate the orthocenters constructed above. As you change the shape of triangle ABC, do the orthocenters of the three embedded triangles change?
Constructing Circumcircles Using Triangle ABC and the Embedded Triangles HBC, HAB, and HAC
Click here for instructions on how to construct the circumcircle of a triangle
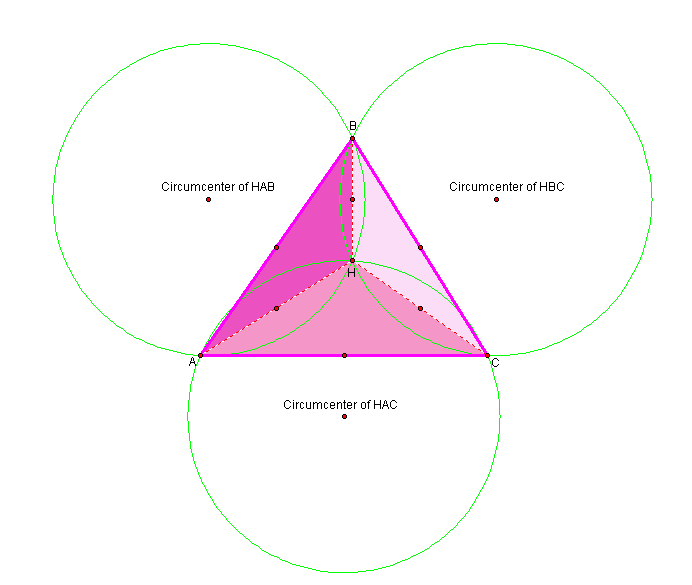
Click here to investigate the circumcircles we have constructed above.