Assignment 9:
Pedal Triangles
The purpose of this assignment is to construct pedal triangles using a point P. We will investigate what happens when point P is:
Any point in the plane of triangle ABC
The Centroid of triangle ABC
The Incenter of triangle ABC
The Orthocenter of triangle ABC (Even if outside of triangle ABC)
The Circumcenter of triangle ABC (Even if outside of triangle ABC)
On a side of the triangle ABC
One of the vertices of triangle ABC
How do you Construct a Pedal Triangle?
First, construct a triangle and a point P. Then extend the sides of the triangle by drawing a parallel line constructed by selecting a side of the triangle and a point on that side. Next, construct perpendicular lines through point P to all of the three sides of the triangle. The vertices of the pedal triangle are the intersection point of the extended parallel lines and the perpendicular lines.
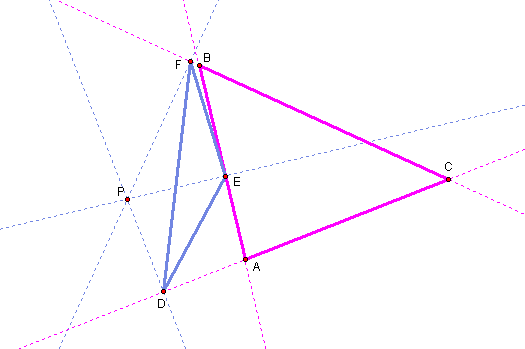
What if Point P is Any point in the plane of triangle ABC?

The pedal triangle constructed from a point P in the plane of the triangle ABC is the blue triangle DEF.
Click here to see what happens when you move point P around in the plane of triangle ABC.
What if Point P is the Centroid of triangle ABC?
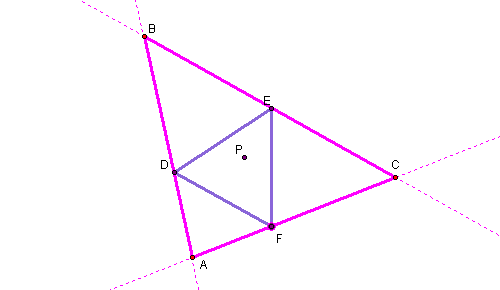
The pedal triangle constructed from point P being the centroid is the purple triangle DEF.
Click here to see what happens to the pedal triangle when you change the shape of the triangle ABC
What if Point P is the Incenter of Triangle ABC?
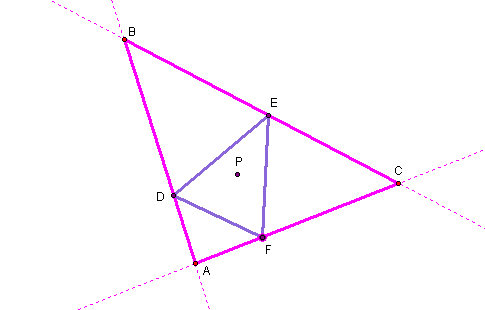
The pedal triangle constructed from point P being the incenter is the purple triangle DEF.
Click here to see what happens to the pedal triangle when you change the shape of the triangle ABC.
What if Point P is the Orthocenter of Triangle ABC?
Even if Outside of Triangle ABC?
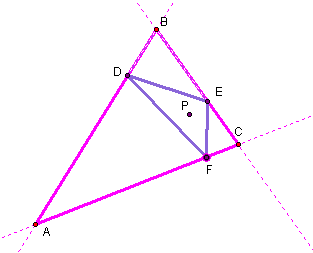
The pedal triangle constructed above from point P being the orthocenter INSIDE triangle ABC is the purple triangle DEF.
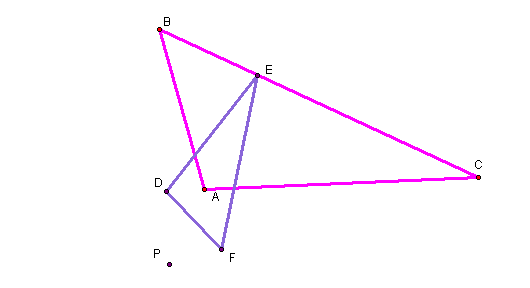
The pedal triangle constructed above from point P being the orthocenter OUTSIDE triangle ABC is the purple triangle DEF.
Click here to see what happens to the pedal triangle when you change the shape of the triangle ABC.
What if Point P is the Circumcenter of Triangle ABC?
Even if Outside of Triangle ABC?

The pedal triangle that has been constructed above from point P being the circumcenter INSIDE triangle ABC is the purple triangle DEF.
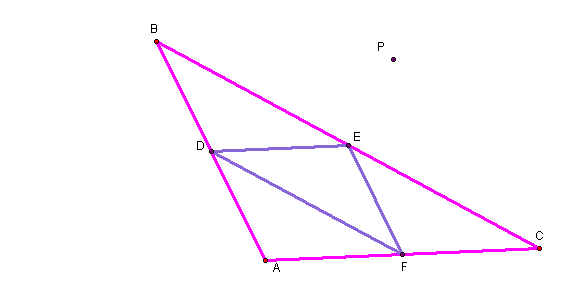
The pedal triangle constructed above from point P being the circumcenter OUTSIDE triangle ABC is the purple triangle DEF.
Click here to see what happens to the pedal triangle when you change the shape of the triangle ABC.
What if Point P is on a Side of the Triangle ABC?
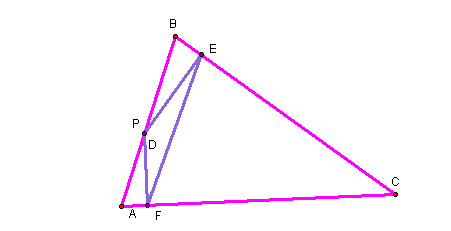
The pedal triangle that has been constructed from point P being on a side of triangle ABC is the purple triangle DEF above.
Click here to see what happens to the pedal triangle when you change the shape of the triangle ABC. Notice that one of the vertices of the pedal triangle is on the side of the triangle ABC.
What if Point P is One of the Vertices of Triangle ABC?
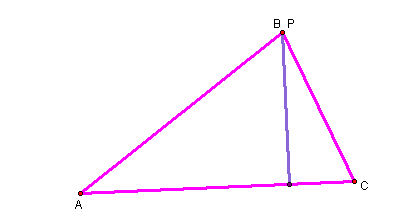
The pedal triangle constructed from point P being one of the vertices of triangle ABC is the purple segment above.
Click here to see what happens to the segment when you change the shape of the triangle ABC.