Assignment 11:
Polar Equations
In this assignment we will be investigating the polar equation:
r = a + b cos (k q)
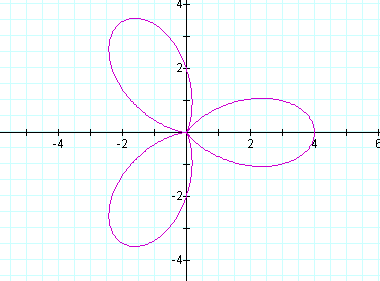
We can begin our investigation by looking at the case when a = b and k is an integer.
This is called the "n-leaf rose".

In the above case, a=b=2 and k=3.
What do you think will happen if a and b are increased?
Click here to see if you are right!
Now Let's Look at what happens when a=b, but we change the value for k
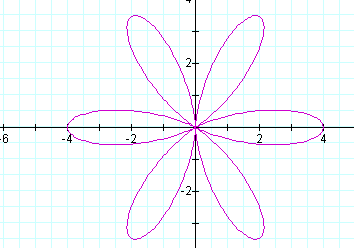
In the above case, a=b=2 and k=6
Are you starting to see a pattern for the value of k?
Click here to see if you are right!
What happens when a=b, but k is NOT an integer?
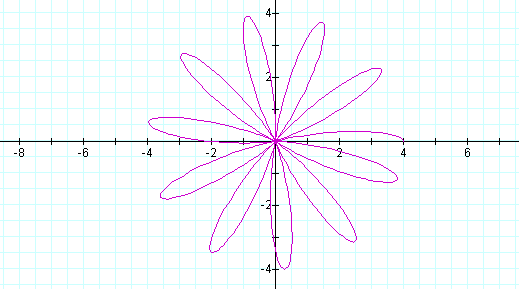
In the above case, a=b=2 and k=10.5
Do you see how k being a non-integer changes the graph?
Click here to see if you are right!
What happens when a and b are not equal?
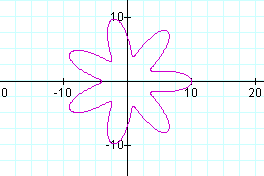
In the above case, a=7, b=3, and k=7
Do you think you see what happens when a and b are not equal?
Click here to see if you are right!
OK ... Now Let's Look at the Equation
r = b cos (k q)
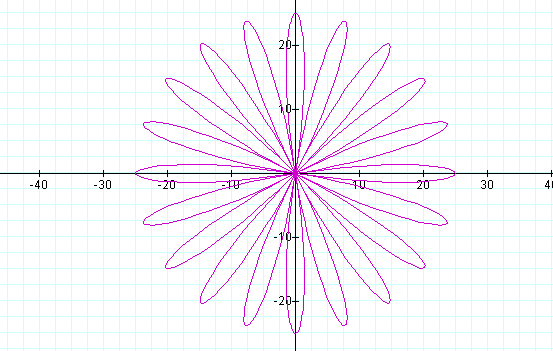
In the above case, b=25 and k=10
Do you see how this equation differs from the first equation?
Click here to see if we have noticed the same thing!
Do you think that if k a non-integer the resulting graph will have half a loop? Click here to see if you are right!
What Do You Think Would Happen if We Replace cos with sin?
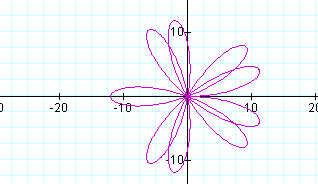
In the above case, b=12 and k=4.5
**NOTICE: When we used cos in the formula when b=12 and k=4.5, the resulting graph had two half loops. Now when we use sin, there are nine full loops (the two half loops have been put together).
What do you think happens when k is an integer?
Click here to check your answer.