Final Assignment
by Laura Evans, UGA
____________________________________
Part A: Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
I started with the following triangle:

______________________________________________________
*Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangle and various locations of P:
Letís look at a few different triangles with different side measures and change the location of P for each. For each of these we will compare the products of (AF)(BD)(EC) and (FB)(DC)(EA) and see of there is any relationship:
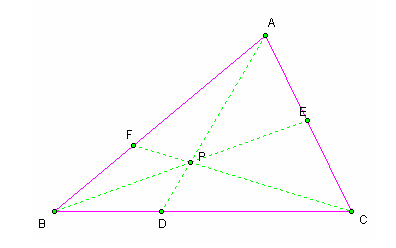
EXAMPLE 1:
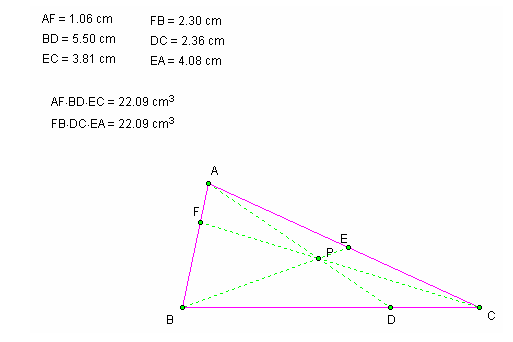
EXAMPLE 2:
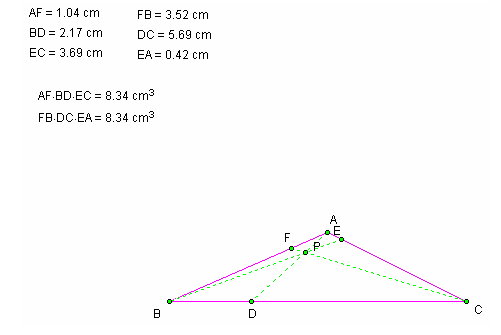
EXAMPLE 3:
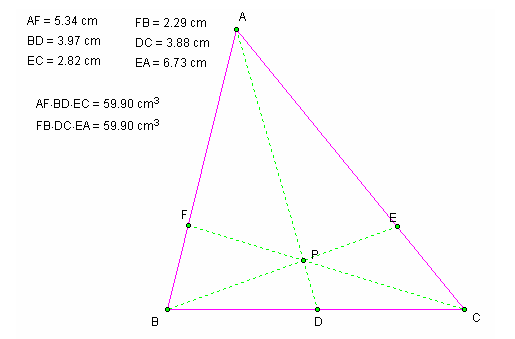
*NOTICE: From these examples we can see that no mater the triangle or the position of P inside the triangle, (AF)(BD)(EC) and (FB)(DC)(EA) are always equal.
______________________________________________________
Part B: Conjecture? Prove it!
Because I have noticed that (AF)(BD)(EC) and (FB)(DC)(EA) are always equal, I would like to make the conjecture that the ratio of these to products is equal to 1.
In order to prove this conjecture, I will need to use similar triangles.
I will need to construct parallel lines: Make two lines that are parallel to segment AD through points B and C.
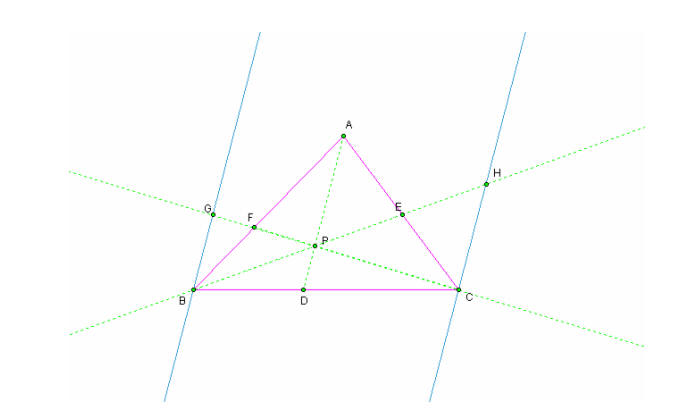
Because I have constructed parallel lines, I can now use the theorem that alternate interior angles of parallel lines are congruent and the theorem that says that vertical angles are congruent.
Now I know that triangles DPC and BGC are similar and triangles BDP and BCH are similar.
By the properties of similar triangles I can set up the following ratios:
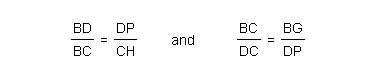
Using the properties of alternate interior angles and vertical angles, I found that triangles BGF and APF are similar and triangles CHE and APE are similar.
By the properties of similar triangles I can set up the following ratios:
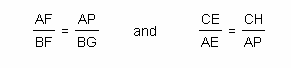
I can now multiply these equations together:
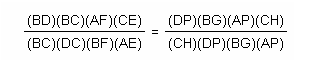
Though algebra and simplifying, the result is:
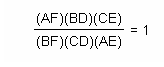
PROOF COMPLETE!!!
______________________________________________________
Part C: Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater then or equal to 4. When is it equal to 4?
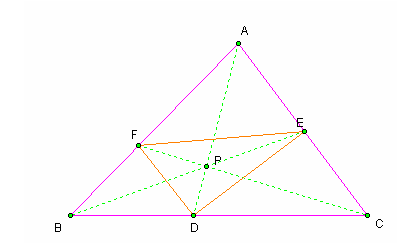
First I will start with triangle ABC with a random point P inside the triangle:
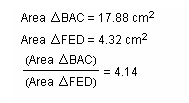
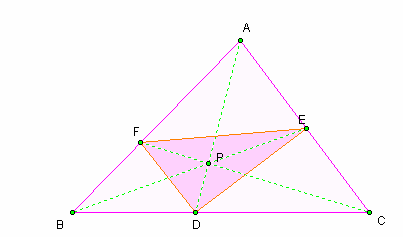
*Notice: The ratio of the areas is greater than 4 when a random point P is chosen inside the triangle.
Now, letís find the centroid of the of triangle ABC, constructing triangle DEF inside triangle ABC:
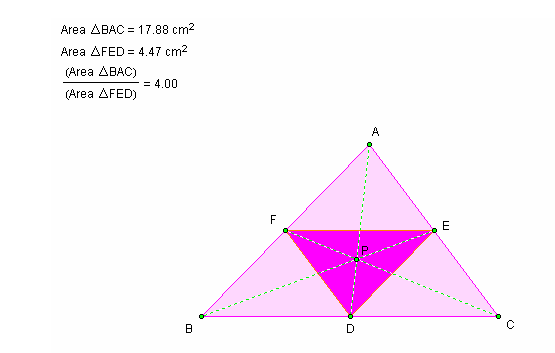
*Notice: When point P is the centroid of the triangle, the ratio of the areas of triangle ABC and DEF is 4.
______________________________________________________